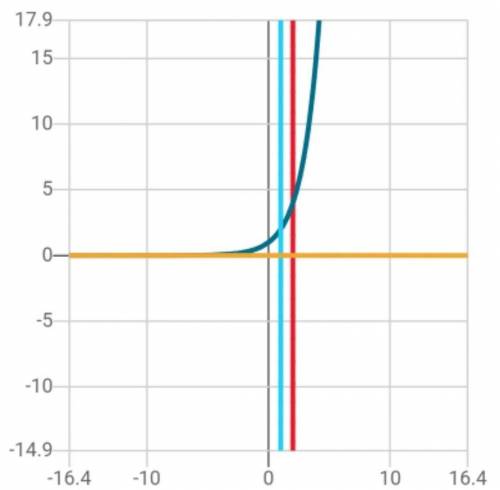
Построим графики функции на одной координатной плоскости (см. приложение).
Увидим кусочек криволинейной трапеции.
Воспользуемся формулой Ньютона-Лейпцина (см. приложение 2)
Получим:
2^x*ln2 |²1
Подставим циферки
2²ln2 - 2¹ln2
Посчитаем, че там у нас получилось
4ln2-2ln2
Благодаря элементарным навыкам в решении математические задач, мы можем польчить следующее
2ln2
И вот чудо, чуть посложнее, конечно, но мы может использовать одну из формул логарифмов
ln4
Не очень красивая площадь вышла, но тем не менее, она равна ln4
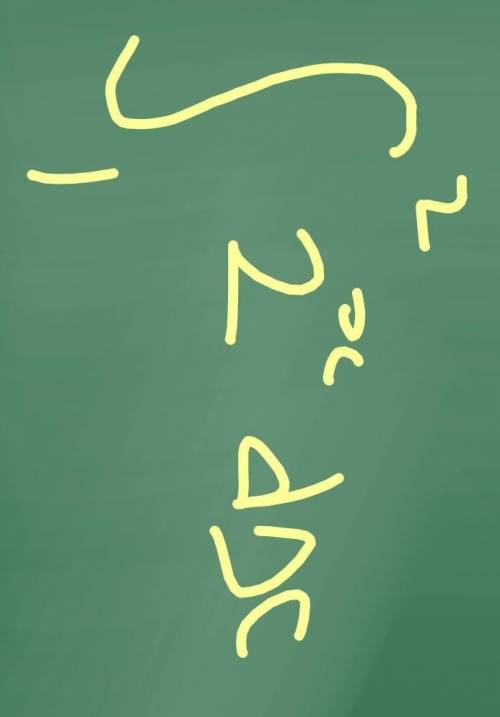
22x-10-17x=55
22x-17x=55+10
5x=65
x=13
б). 5(8х+3)-12=83
40х+15-12=83
40х=83-3
х=2
в). 7(2х+9)+3х=114
14х+63+3х=114
17х=114-63
17х= 51
х=3
г). 3(4х+13)-25=74
12х+39-25=74
12х=74-14
12х=60
х=5