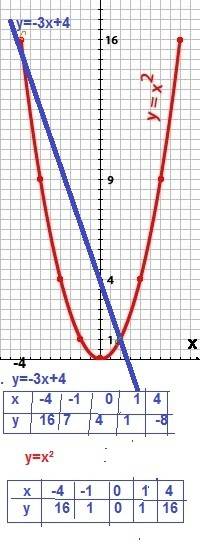
x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно
x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно

1) Обрати дві різних непарних цифри ми можемо .
2) Розглянемо два випадки: серед шуканої пари парних чисел немає нуля, таких
варіантів C2/4 серед шуканої пари парних цифр є нулем, таких варіантівC1/4
3) Четвірок цифр, серед яких дві цифри непарні, дві парні й немає нуля маємо
C 2/5*C 2/4 . Перестановка цифр у кожній четвірці відповідає різним числам. Таких 54
перестановок маємо Р4 = 4!. Отже чисел шуканого виду буде
C 2/5*C 2/4 *4! = 10*6*24=1440. 54
4) Четвірок цифр, серед яких дві цифри непарні, нуль і одна парна відмінна від нуля,
маємо C 2/5*C 1/4 . Перестановка цифр у кожній четвірці відповідає різним
чотирицифровим числам, окрім випадку, коли на першому місці стоїть нуль .Таких перестановок маємо Р4 – Р3 = 4! – 3!. Отже чисел шуканого виду буде
C2/5*C1/4 (4!–3!)=10*4*(24-6)=720.
5) Загалом чотиризначних чисел, в яких дві цифри парні, а дві – непарні існує 1440 + 720 = 2160.
Відповідь: 2160.