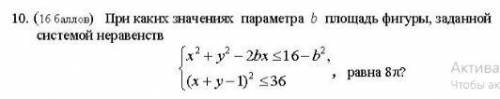
эта музыка насыщена маршевыми интонациями. Музыка «Военного марша» звучит бодро, энергично, торжественно.
Какое выразительное значение имеет вступление к маршу?
Звучание трубы напоминает «военные сигналы» и тем самым создает особое боевое приподнятое настроение и сильный характер.
: Обе мелодии маршевого характера, слышится четкий шаг, но вторая мелодия более напевная, что вносит контраст образов.
Марш написан в трехчастной форме. И мелодия первой и третьей части закрепляет значимость образных характеристик марша: торжественно победного
a) sin(a-pi)=-sin a
cos(a-3pi/2)=-sin a
ctg(a-pi/2)=-tg a=-sin a/cos a
tg(pi+a)=tg a=sin a/cos a
sin(a-pi)+cos(a-3pi/2)/ctg(a-pi/2)-tg(pi+a) =-sin a + (sin a *cos a)/sin a + tg a = -sin a + cos a + tg a
б)
cos(3pi/2-a)=-sin a
cos(6pi-a)=cos a
sin(a+8pi)=sin a
sin(3pi/2+a) =-cos a
Если cos(6п-a)/1+sin(a+8п) - это cos(6п-a)/(1+sin(a+8п)), то
1-cos(3pi/2-a)+cos(6pi-a)/(1+sin(a+8pi))-sin(3pi/2+a)=1+sin a+cos a/(1+sina)
Если cos(6п-a)/1+sin(a+8п) как то по другому, то смотри сам. Думаю +, -, * и / впихнешь как-то.
в) tg(pi+a)=tg a
tg(5pi/2-a)=ctg a
sin(pi/2-a)=cos a
tg a* ctg a=1
cosa*tg(pi+a)*tg(5pi/2-a)/sin(pi/2-a)-1=cos a * tg a* ctg a/cos a -1 = cos a/cos a - 1 =1-1=0
Все решается с формул приведения.
Пошаговое объяснение:
Пошаговое объяснение:
Для начала рассмотри первое неравенство системы, оно похоже на функцию окружности. Преобразуем это неравенство и посмотрим:
Теперь рассмотрим второе неравенство системы, попробуем его преобразовать:
Из этой системы неравенств можем записать двойное неравенство:
Во втором случаем будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые
будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые 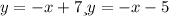 с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
Теперь разберемся с первым неравенством системы: Поскольку это окружность радиуса 4, то ее площадь будет равна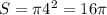 . Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна
. Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна 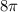 , т.е половина окружности. Отсюда становится понятно что ее площадь будет равна
, т.е половина окружности. Отсюда становится понятно что ее площадь будет равна 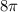 (т.е половине) в той точке, где прямая отсечет от нее половину.
(т.е половине) в той точке, где прямая отсечет от нее половину.
В случае с прямой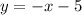 , то значение параметра
, то значение параметра 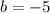 , тогда окружность становится на точку -5 по оси абсцисс, где прямая
, тогда окружность становится на точку -5 по оси абсцисс, где прямая 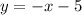 пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых 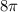 , значит
, значит 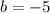 решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
В случае с прямой В случае с прямой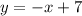 , то значение параметра
, то значение параметра 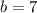 , тогда окружность становится на точку 7 по оси абсцисс, где прямая
, тогда окружность становится на точку 7 по оси абсцисс, где прямая 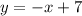 пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых 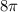 , значит
, значит 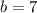 решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
Получаем