
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:x - (-1) y - 4 z - 3
3 - (-1) 6 - 4 2 - 3
2 - (-1) (-5) - 4 (-3) - 3 = 0
x - (-1) y - 4 z - 3
4 2 -1
3 -9 -6 = 0
(x - (-1))*(2·(-6)-(-1)·(-9)) - (y - 4)*(4·(-6)-(-1)·3) + (z - 3)*(4·(-9)-2·3) = 0
(-21)x - (-1) + 21y - 4 + (-42)z - 3 = 0
- 21x + 21y - 42z + 21 = 0
x - y + 2z - 1 = 0
Пошаговое объяснение:
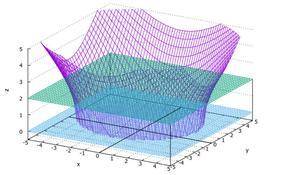
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
 , где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
, где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс

теперь нам надо каноническое уравнение нашего эллипса
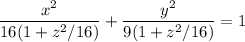
упростим

площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
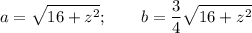
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем

(см. объяснение)
Пошаговое объяснение:
Заметим, что является корнем уравнения при любом значении параметра. Тогда нужно, чтобы уравнение
является корнем уравнения при любом значении параметра. Тогда нужно, чтобы уравнение  имело ровно один корень принадлежащий ОДЗ и не равный двум.
имело ровно один корень принадлежащий ОДЗ и не равный двум.
Введем замену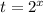 . Откуда
. Откуда 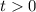 .
.
Тогда уравнение примет вид:
Переформулируем условие задачи:
Найти все значение параметра , при каждом из которых записанное выше уравнение имеет ровно один корень, принадлежащий промежутку
, при каждом из которых записанное выше уравнение имеет ровно один корень, принадлежащий промежутку  .
.
Введем функцию . Это парабола, ветви которой направлены вверх, а координата вершины имеет значение
. Это парабола, ветви которой направлены вверх, а координата вершины имеет значение  .
.
Отрисовав возможные расположения парабол, учитывая расположение ее вершины, перейдем к системам:
(я рисовать их не буду, так как на компьютере это неудобно + вы говорите, что уже сами задачу решили)
Выполним необходимые вычисления:
Тогда записи примут вид:
Итого при![a\in\left(-1;\;0\right]\cup\left\{\dfrac{3}{2}\right\}\cup\left[3;\;4\right)](/tpl/images/2009/9621/e2fe0.png) исходное уравнение имеет ровно два различных корня.
исходное уравнение имеет ровно два различных корня.
Задание выполнено!