Y=11x+ln =11x+11 ln(x+15) Для нахождения наименьшего значения функции находим первую производную данной функции y ' =(11x +ln) ' =11+ 11 = = Решаем уравнение (находим критические точки) y '=0 11x+154=0 ⇒ 11x = - 154 ⇒ x= - 154/11 = -14 При x < -14 производная функции отрицательна (функция убывает), при x > -14 производная функции положительна (функция возрастает), значит в критической точке x = -14 функция принимает минимум, найдем это значение y(-14) =11*(-14) - 11ln(-14+15) = -154 -11*ln 1 = -154 -11*0= -154 ответ: -154
Рисуем прямоугольник АВСК , проводим диагональ АС (в прямоугольнике диагонали одинаковы ) . АВ=СК=х см , значит ВС=АК=12/х см (т.к. S = а*в) . Р прям. = 2(а+в)=2*(х+12/х)=14 , приводим у общему знаменателю : 2х^2+24=14х 2х^2-14х+24=0 D=196-192=4=2^2 Х=(14-2)/4=3 или (14+2)/4=4 Разницы какой х Вы возьмете нету , потому что если будет 3 то другая сторона будет 12/3=4 , а если - 4 , то другая - 12/4=3 ( что так , что так будет 3 и 4) , теперь смотрим на треугольник АСК , АС=корень из ( 9+16) = 5 см
ответ: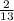
Пошаговое объяснение:
Пока не будем обращать внимание на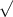 , для начала посчитаем основание корня.
, для начала посчитаем основание корня.
1)
2)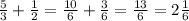
3)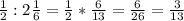
4)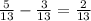
По итогу, получаем: