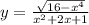
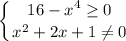
1)16-x⁴≥0 , (4-x²)(4+x²)≥0 ,(2-x)(2+x)(4-x²)≥0 , нули х=2,х=-2 ,4+x²>0 при любом х . Метод интервалов - - - - - - -[-2]+ + + + +[2]- - - - - - - ,
х∈[-2;2]
2)x²+2x+1≠0
(x+1)²≠0 , x≠-1
3) х∈[-2;2] и x≠-1
количество целых значений аргумента 4. Это -2,0,1,2
Нерівність 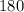 ÷
÷  вірно при
вірно при 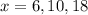 і невірно при
і невірно при  .
.
Для того, щоб перевірити правильність рішення, треба зробити такі покрокові рішення:
1) Число 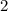 :
:
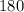 ÷
÷ 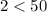
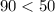
Висновок: число 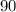 більше, ніж
більше, ніж  , а не менше, отже, таку нерівність нвеерно при значенні х, якому дорівнює
, а не менше, отже, таку нерівність нвеерно при значенні х, якому дорівнює 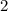 .
.
2) Число 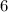 :
:
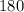 ÷
÷ 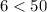

Висновок: число 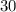 менше
менше  , тому, нерівність при х, значення якого дорівнює
, тому, нерівність при х, значення якого дорівнює 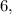 вірно.
вірно.
3) Число 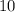 :
:
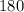 ÷
÷ 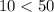

Висновок: число 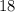 менше
менше  , тому при цьому нерівність теж вірно.
, тому при цьому нерівність теж вірно.
4) Число 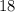 :
:
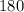 ÷
÷ 
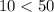
Висновок: число 10 менше 50, так що, нерівність виходить теж вірним.
Підсумковий висновок: числа  є рішенням вищевказаного нерівності, а число [/tex]2 не є вирішенням цього рівності.
є рішенням вищевказаного нерівності, а число [/tex]2 не є вирішенням цього рівності.
1. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза меньше, а третья- в 2 раза меньше второй:
4:2=2(см)- радиус второй окружности;
2:2=1(см)- радиус третий окружности.
радиус = 1, 2, 4
2. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза меньше, а третья- в 2 раза больше:
4:2=2(см)- радиус второй окружности;
4*2=8(см)- радиус третий окружности.
радиус - 2, 4, 8
3. если радиус одной из окружностей равен 4 см, то вторая окружность может быть в 2 раза больше, а третья- в 2 раза больше второй:
4*2=8(см)- радиус второй окружности;
8*2=16(см)-радиус третий окружности.
радиус = 4, 8, 16
4 целых значений аргумента -2; 0; 1; 2
Пошаговое объяснение:
y=√(16-x⁴)/(x²+2x+1)
1) 16-x⁴≥0
x⁴≤16
|x|≤2
-2≤x≤2
2) 0≠x²+2x+1=(x+1)²⇒x+1≠0⇒x≠-1
3) D(y)={x| x∈Z, z∈[-2;2], x≠-1}⇒D(y)={-2; 0; 1; 2}