∠АВН = 30°; ∠ВАР = 45°.
Пошаговое объяснение:
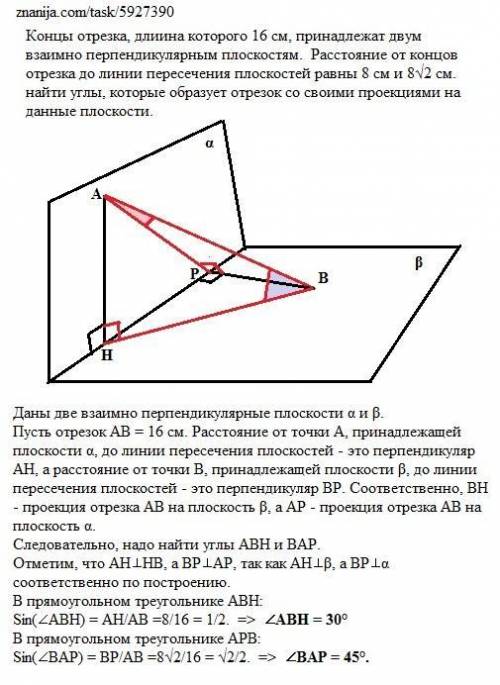
Концы отрезка, длина которого 16 см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояние от концов отрезка до линии пересечения плоскостей равны 8 см и 8√2 см. найти углы, которые образует отрезок со своими проекциями на данные плоскости.
Решение.
Даны две взаимно перпендикулярные плоскости α и β.
Пусть отрезок АВ = 16 см. Расстояние от точки А, принадлежащей плоскости α, до линии пересечения плоскостей - это перпендикуляр АН, а расстояние от точки В, принадлежащей плоскости β, до линии пересечения плоскостей - это перпендикуляр ВР. Соответственно, ВН - проекция отрезка АВ на плоскость β, а АР - проекция отрезка АВ на плоскость α.
Следовательно, надо найти углы АВН и ВАР.
Отметим, что АН⊥НВ, а ВР⊥АР, так как АН⊥β, а ВР⊥α соответственно по построению.
В прямоугольном треугольнике АВН:
Sin(∠АВН) = АН/АВ =8/16 = 1/2. => ∠АВН = 30°
В прямоугольном треугольнике АРВ:
Sin(∠ВАР) = ВР/АВ =8√2/16 = √2/2. => ∠ВАР = 45°.
Пошаговое объяснение:
Не сказано с повторениями или нет.
1) Если в условии сказано, что каждая цифра используется единожды, тогда кол-во четырёхзначных чисел из цифр 3, 4, 5, 6 будет 4!=24.
чисел заканчивающихся на 36 будет 2!=2
24-2=22
2) Если в условии сказано, что каждая цифра используется по нескольку раз(например 3344), тогда кол-во четырёхзначных чисел из цифр 3, 4, 5, 6 будет 4⁴=256.
чисел заканчивающихся на 36 будет 4²=16
256-16=240