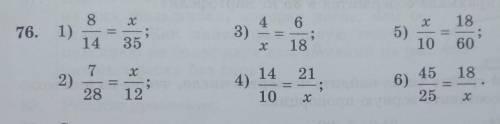
1) 8/14=х/35 = 40/70=x/70. x=20
2)7/28=x/12 = 21/84=x/84. x=3
3)4/x=6/18 = 12/x=12/36. x=12
4)14/10=21/x = 42/30=42/x. x=15
5)x/10=18/60 = x/60=18/60. x=3
6)45/25=18x = 90/50=90/x. x=10
Пошаговое объяснение:
В треугольнике АВС, ВК - биссектриса угла В(Угол КВС=Угол АВК). Т.к синус угла А равен 0.5, угол А равен 30 градусов( в интернете есть куча таблиц).
Т.к угол А равен 30 градусов, угол В равен 60 градусов (сумма острых углов в прямоугольном треугольнике 90 градусов!) и углы КВС и АВК равны 30 градусам.В треугольнике КВС, т.к КС лежит против угла 30 градусов, она равна половине гипотенузы(ВК)=2 корня из 3.В данном треугольнике по теореме Пифагора находим, что ВС = 6 см.В треугольнике АВС, синус А=0.5, синус А = ВС/АВ=6/АВ. 6/АВ=0.5 АВ = 12 см.
Пошаговое объяснение:
Расстояние между городами 584 км.
Направление движения: на встречу друг другу.
Выехали из двух городов одновременно.
Скорость грузового автомобиля на 16 км/ч больше автобуса.
Время движения 4 ч.
Определить скорость грузового автомобиля и автобуса.
Пусть скорость автобуса равна х км/ч, тогда скорость грузового автомобиля будет (х + 16) км/ч.
Расстояние, на которое сближаются грузовой автомобиль, и автобус за единицу времени, называют скоростью сближения vсб.
В случае движения грузового автомобиля и автобуса навстречу друг другу, скоростью сближения равно: vсб = v1 + v2
Если начальная расстояние S между грузовым автомобилем и автобусом равна 584 километров и они встретились через tвст = 4 ч, то S = vсб * tвст = (v1 + v2) * tвст
Составим уравнение:
(х + (х + 16)) * 4 = 584
(2х + 16) * 4 = 584
8х + 64 = 584
8х = 584 – 64
8х = 520
х = 520 : 8
х = 65
Скорость автобуса равно 65 км/ч.
Скорость грузового автомобиля равно 65 + 16 = 81 км/ч.
ответ: скорость автобуса — 65 км/ч; скорость грузовой машины — 81 км/ч.
1) х=8*35:14 х=20
2) х=7*12:28 х=3
3) х=4*18:6 х=12
4) х=10*21:14 х=15
5) х=10*18:60 х=3
6) х=25*18:45 х=10