
Пошаговое объяснение:
Чтобы решить данную задачу - нужно помнить теорию о тригонометрических функция:
Рассмотрим треугольник АВС:
1. Он равнобедренный
2. Разделён на два прямоугольных треугольника
3. Проведена медиана AK
a) Теперь найдём синус угла А или sin ∠A:
Рассмотрим ΔABH:
AB=10 и AH=1/2*AC=6
sin ∠A находится через отношения :
sin ∠A = BH/AB
Найдём BH через теорему Пифагора:
BH = 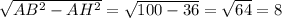
И вычислим синус :
sin ∠A = 8/10 =0,8
b) Косинус находится через отношение п:
cos ∠C = HC/BC
Подставим значения:
cos ∠C = 10/6=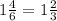
в) Тангенс угла CBH находится отношением:
tg ∠CBH = BH/HC
Подставим значения:
tg ∠CBH = 8/6=4/3=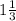
г) Найдём сначала синус угла ABC
Найдём синусы углов ABH и HBC:
sin ABH =AH/AB ; sin HBC = HC/BC
sin ABH = 0,6 ; sin HBC = 0,6
sin ABC = sin ABH + sin HBC =1,2
Заметим sin ABC=sin ABK =1,2 ,поэтому найдём высоту AK:
sin HBC = AK/AB => AK=sin HBC * AB => AK=1,2*10=12
Пошаговое объяснение:
Щоб позначити точки М(3; -2), К(-1; -1) і С(0; 3) на координатній площині, ми використовуємо вісі X і Y. Вісь X горизонтальна, а вісь Y вертикальна.
Точка М(3; -2) має координати (3, -2). Ми позначимо її на площині, малюючи точку у третьому квадранті, зміщену вправо на 3 одиниці і вниз на 2 одиниці.
Точка К(-1; -1) має координати (-1, -1). Ми позначимо її на площині, малюючи точку в другому квадранті, зміщену вліво на 1 одиницю і вниз на 1 одиницю.
Точка С(0; 3) має координати (0, 3). Ми позначимо її на площині, малюючи точку в першому квадранті, на висоті 3 одиниці.
Отже, ми позначили всі три точки на координатній площині.
Тепер давайте проведемо пряму МК через точки М і К. Пряма МК буде лінією, що проходить через ці дві точки.
Для проведення прямої, ми з'єднаємо точку М(3; -2) і точку К(-1; -1) лінією.
Щоб провести пряму, паралельну МК через точку С, ми використовуємо факт, що паралельні прямі мають однаковий нахил (коефіцієнт пропорційності) і не перетинаються. Оскільки МК має певний нахил, паралельна пряма, проведена через точку С, також матиме цей самий нахил. Тому ми проведемо пряму, що проходить через точку С(0; 3) і має такий самий нахил, як пряма МК.
Щоб провести пряму, перпендикулярну до МК через точку С, ми використовуємо факт, що перпендикулярні прямі мають взаємно обернений нахил. Оскільки МК має певний нахил, пряма, перпендикулярна до МК, матиме взаємно обернений нахил. Тому ми проведемо пряму, що проходить через точку С(0; 3) і перпендикулярна до прямої МК.