ДОМАШНЕЕ ЗАДАНИЕ 21 Вычисли. 4 см. ПОНЕ НА ОВ ОБЪЯСН а) Узнай объем коробки, если ее длина 12 см, ширина - 7 см, высота 6) Найди сумму площадей боковых граней и дна данной коробки. в) Узнай в различных источниках возможные размеры аквариумов. Вычисли их объём.

👇

Увидеть ответ

Открыть все ответы

Ответ:

шота1

16.09.2021

S = a · b - формула площади прямоугольника

Пусть а₁ = х - ширина, тогда b₁ = 3х - длина

S = х · 3х = 3х² - первоначальная площадь

а₂ = (х - 2) - ширина, b₂ = 3х - длина

S = (х - 2) · 3х = 3х² - 6х - площадь после уменьшения ширины

Уравнение:

3х² - (3х² - 6х) = 42

3х² - 3х² + 6х = 42

6х = 42

х = 42 : 6

х = 7 (м) - ширина а

3х = 3 · 7 = 21 (м) - длина b

Вiдповiдь: 21 м - початкова довжина прямокутника.

Проверка:

7 · 21 = 147 м² - первоначальная площадь

(7 - 2) · 21 = 5 · 21 = 105 м² - площадь после уменьшения ширины

147 - 105 = 42 м² - разница

4,6(27 оценок)

Ответ:

viktoriya2000ok

16.09.2021

Будем разбивать на несколько случаев.

1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 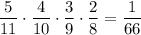$\dfrac{5}{11}\cdot \dfrac{4}{10}\cdot \dfrac{3}{9}\cdot\dfrac{2}{8}=\dfrac{1}{66}$ . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна $\dfrac{3}{12}\cdot\dfrac{2}{11}\cdot\dfrac{1}{10}=\dfrac{1}{220}$ . 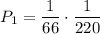По теореме умножения $P_1=\dfrac{1}{66}\cdot\dfrac{1}{220}$

2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 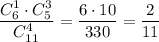$\dfrac{C^1_6\cdot C^3_5}{C^4_{11}}=\dfrac{6\cdot10}{330}=\dfrac{2}{11}$ . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 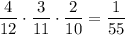$\dfrac{4}{12}\cdot\dfrac{3}{11}\cdot\dfrac{2}{10}=\dfrac{1}{55}$ . По теореме умножения: $P_2=\dfrac{2}{11}\cdot\dfrac{1}{55}$

3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 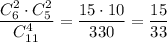$\dfrac{C^2_6\cdot C^2_5}{C^4_{11}}=\dfrac{15\cdot10}{330}=\dfrac{15}{33}$ . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 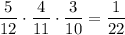$\dfrac{5}{12}\cdot\dfrac{4}{11}\cdot\dfrac{3}{10}=\dfrac{1}{22}$ . По теореме умножения : $P_3=\dfrac{15}{33}\cdot\dfrac{1}{22}$

4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна $\dfrac{C^3_6\cdot C^1_5}{C^4_{11}}=\dfrac{20\cdot5}{330}=\dfrac{10}{33}$ . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна $\dfrac{6}{12}\cdot\dfrac{5}{11}\cdot\dfrac{4}{10}=\dfrac{1}{11}$ . 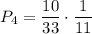По теореме умножения: $P_4=\dfrac{10}{33}\cdot\dfrac{1}{11}$

5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 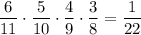$\dfrac{6}{11}\cdot\dfrac{5}{10}\cdot\dfrac{4}{9}\cdot\dfrac{3}{8}=\dfrac{1}{22}$ . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 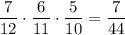$\dfrac{7}{12}\cdot\dfrac{6}{11}\cdot\dfrac{5}{10}=\dfrac{7}{44}$ . По теореме умножения: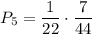 $P_5=\dfrac{1}{22}\cdot\dfrac{7}{44}$

Итого, по теореме сложения:

$P=P_1+P_2+P_3+P_4+P_5=\dfrac{1}{66}\cdot\dfrac{1}{220}+\dfrac{2}{11}\cdot\dfrac{1}{55}+\dfrac{15}{33}\cdot\dfrac{1}{22}+\\ \\ +\dfrac{10}{33}\cdot\dfrac{1}{11}+\dfrac{1}{22}\cdot\dfrac{7}{44}=\dfrac{427}{7260}\approx 0{,}0588$