Пошаговое объяснение:
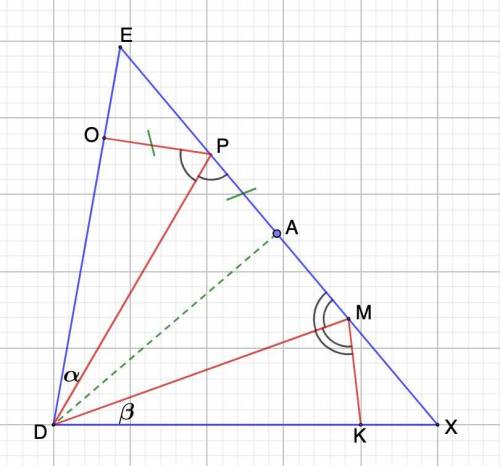
Дано: ΔDEX;
∠EDX = 2∠PDM;
∠OPD = ∠DPX; ∠KMD = ∠DME;
Доказать: OP + KM = PM
Доказательство:
Дополнительное построение.
Отложим отрезок РА = РО.
1. Рассмотрим ΔDOP и ΔDPA.
PA = PO (построение);
∠OPD = ∠DPX (условие)
DP - общая.
⇒ ΔDOP = ΔDPA (по двум сторонам и углу между ними. 1 признак)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠ODP = ∠PDA
2. Пусть ∠ODP = α, а ∠MDX = β.
∠EDX = 2∠PDM (по условию)
⇒ ∠PDM = α + β
∠ODP = ∠PDA = α (п.1)
⇒ ∠ADM = ∠PDM - ∠PDA = α + β - α = β
3. Рассмотрим ΔDAM и ΔDMK.
∠ADM = ∠MDK = β (п.2)
∠KMD = ∠DME (условие)
DM - общая.
⇒ ΔDAM = ΔDMK (по стороне и двум прилежащим углам. 2 признак)
В равных треугольниках против равных углов лежат равные стороны.⇒ АМ = МК
4. РМ = РА + АМ или РМ = PO + KM.
На сторонах AB и BC треугольника ADC взяты точки D и E соответственно так, что AD:BD = 1:2 и CE:BE = 2:1. Отрезки AE и CD пересекаются в точке O. Найти площадь треугольника ABC, если площадь треугольника BCO равна 1.
Рассмотрим ∆ АВЕ.
По т Менелая (ВD:DA)•(AO:OE)•(CE:CB)=1
2/1•(AO:OE)•2/3=1, откуда АО:ОЕ=3:4
ОЕ делит ВС в отношении 1:2, считая от В.
Высота ∆ СОЕ и ∆ СОВ общая.
Отношение площадей треугольников с равными высотами равно отношению их оснований. СЕ:СВ=2/3⇒
Ѕ(ВОС)=1, значит, Ѕ(СОЕ)=2/3
В ∆ АСЕ отрезок СО делит АЕ в отношении 3:4, считая от А.
Высота ∆ АСЕ и ∆ СОЕ, проведенная из вершины С, общая.
Тогда Ѕ(САЕ)=2/3:4•7=7/6
Высота ∆ АВС и ∆ АСЕ общая.⇒
Ѕ АВС=Ѕ(АСЕ):2•3=(7/6):2•3=7/4
Пошаговое объяснение:
ответ - 12 и 15