Відрізок AB перетинає площину а. Через точки A, B і М — середину відрізка — проведено паралельні прямі, що перетинають площину а у точках A, B, і М1, відповідно. Знайдіть MМ1, якщо АА1, = 3 см, BB1 = 17 см.
Все точки () лежат на одной плоскости обозначим её β, таким образом можно рассматривать аналогию в планиметрии. Плоскость β пересекается с плоскостью α по прямой на которой лежат точки . Обозначим эту прямую . Проведем параллельную прямую которая проходит через точку . Пусть прямая проходящая через точки и пересечет в точке , и пусть прямая проходящая через точки и пересечет прямую в точке . По признаку параллелограмма следует, что четырехугольник - параллелограмм откуда имеем, что см. Отрезок - средняя линия треугольника , откуда имеем, что см. Нетрудно узреть, что см. Таким образом см
Не верно рассматривать только одну последовательность ,что школьники сядут только на 18 ,19 и 20 ,Здесь возможно много вариантов пусть номера школьников 1, 2, 3 те 3 школьника и 3 места 18 ,19 и20 .Например школьник 1 может сесть на 18,19 или 20 место ,тогда школьник 2 может сесть на любое из двух свободных мест,а школьник 3 уже сможет сесть на дно оставшееся место.Например ,школьник 1 займет место номер 18 ,тогда школьник 2 может занять место номер19 ,или номер 20 ,и если он займет место 19 ,то школьник 3 вынужден занят 20 место , а если школьник 2 займет 20 место ,то школьнику останентся 19 место -вот вам 2 варианта, теперь рассмотрите вариант ,если школьник 1 займет место 19 ,и аналогично рассуждайте относительно двух других получаем -еще 2 варианта ,теперь пусть школьник 1 займет место 20 и так снова вариантов- два, значит количество возможных размещений трех школьников на трех местах равно 6! Это число перестановок.Пример: 1-18 место, 2- 19 место, 3-20 место,либо 1-18,2-20, 3-19.это 2 варианта,теперь 1-19, 2-18,3-20 или 1-19, 2-20, 3-18 -снова 2 варианта и последнее 1-20 ,2-18 ,3-19 или 1-20, 2-19 ,3-18 еще 2 варианта всего -6.
Не верно рассматривать только одну последовательность ,что школьники сядут только на 18 ,19 и 20 ,Здесь возможно много вариантов пусть номера школьников 1, 2, 3 те 3 школьника и 3 места 18 ,19 и20 .Например школьник 1 может сесть на 18,19 или 20 место ,тогда школьник 2 может сесть на любое из двух свободных мест,а школьник 3 уже сможет сесть на дно оставшееся место.Например ,школьник 1 займет место номер 18 ,тогда школьник 2 может занять место номер19 ,или номер 20 ,и если он займет место 19 ,то школьник 3 вынужден занят 20 место , а если школьник 2 займет 20 место ,то школьнику останентся 19 место -вот вам 2 варианта, теперь рассмотрите вариант ,если школьник 1 займет место 19 ,и аналогично рассуждайте относительно двух других получаем -еще 2 варианта ,теперь пусть школьник 1 займет место 20 и так снова вариантов- два, значит количество возможных размещений трех школьников на трех местах равно 6! Это число перестановок.Пример: 1-18 место, 2- 19 место, 3-20 место,либо 1-18,2-20, 3-19.это 2 варианта,теперь 1-19, 2-18,3-20 или 1-19, 2-20, 3-18 -снова 2 варианта и последнее 1-20 ,2-18 ,3-19 или 1-20, 2-19 ,3-18 еще 2 варианта всего -6.
Пошаговое объяснение:
Все точки (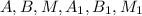
) лежат на одной плоскости обозначим её β, таким образом можно рассматривать аналогию в планиметрии. Плоскость β пересекается с плоскостью α по прямой на которой лежат точки 
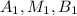. Обозначим эту прямую 
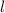. Проведем параллельную прямую 
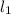которая проходит через точку 
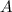. Пусть прямая проходящая через точки 
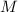и 
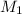пересечет 
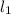в точке 
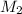, и пусть прямая проходящая через точк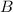и 
и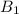 
пересечет прямую 
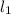в точке 
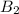. По признаку параллелограмма следует, что четырехугольник 
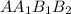- параллелограмм откуда имеем, что 
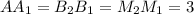см. Отрезок 
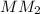- средняя линия треугольника 
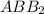, откуда имеем, что 
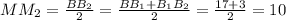см. Нетрудно узреть, что 
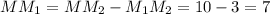см. Таким образом 
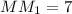см