4 см
Пошаговое объяснение:
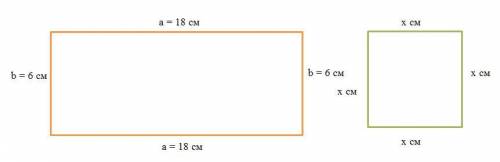
Дано (см. рисунок):
длина прямоугольника a = 18 см
ширина прямоугольника b = 6 см
периметр квадрата составляет третью часть периметра прямоугольника
Найти: сторону квадрата х.
Решение.
Периметр Р(прямоугольник) прямоугольника длиной a и шириной b определяется по формуле
Р(прямоугольник) = 2·(a + b) .
На основе заданных:
Р(прямоугольник) = 2·(18 см + 6 см) = 2·24 см = 48 см
Периметр Р(квадрат) квадрата стороной х определяется по формуле
Р(квадрат) = 4 · х.
По условию периметр Р(квадрат) квадрата составляет третью часть периметра прямоугольника, поэтому
Р(квадрат) = Р(прямоугольник) : 3 = 48 см : 3 = 16 см.
Тогда из следующих равенств можем определить сторону х квадрата:
P(квадрат) = 4 · х и P(квадрат) = 16 см
4 · х = 16 см
х = 16 : 4 см = 4 см
ответ: 4 см
24/30 = 4/5
28/32 = 7/8
21/35 = 3/5
75/45 = 5/3 = 1целая 2/3
38/66 = 19/33
54/90 = 27/45 = 9/15 = 3/5
36/84 = 18/42 = 9/21 = 3/7
49/56 = 7/8
55/77 = 5/7
26/65 = 2/5
51/85 = 3/5