Получили разные значения - бездоказательно.
Пошаговое объяснение:
Пусть имеем число 100
30% = 0,3 40% = 0,4 70% = 0,7
100 - 100*0,3х = 100 - 30 = 70 - число уменьшили на 30%
70 - 70*0,4 = 70 - 28 = 42 - число уменьшили ещё на 40%
Далее:
100 - 100*0,7 = 100 - 70 = 30 - число сразу уменьшили на 70%
Получили разные значения - бездоказательно.
Одно и тоже число получится при условии, если сначала это число уменьшить на 30%, а затем это же число уменьшить на 40% и из этого числа вычесть их сумму:
100 - (100*0,3 + 100*0,4) = 100 - (30 + 40) = 30
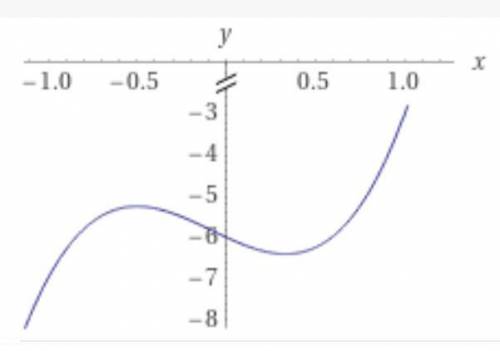
Дана функция f(x)=4x³+x²-2x-6.
Её производная равна: y' = 12x²+2x-2.
Приравняем производную нулю: 12x²+2x-2 = 0, 2(6x²+x-1) = 0.
Д = 1+24 = 25, х1 = (-1-5)/12 = -1/2, х2 = (-1 + 5)/12 = 4/12 = 1/3.
Найдены 2 критические точки: х1 = (-1/2) и х2 =(1/3).
Находим значения производной на полученных промежутках:
х ∈ ( -∞;(-1/2) ) ((-1/2);(1/3)) ((1/3);+∞).
х = -1 (-1/2) 0 ( 1/3) 1
y' = 8 0 -2 0 12.
Ф_ция ↑ max ↓ min ↑
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
За 6 часов.
Пошаговое объяснение:
Запишем всю работу, которую должны выполнить мастера ка 1.
В таком случае, продуктивность первого мастера была равна:
1 / 10 = 1/10 часть работы в час.
Находим продуктивность работы второго мастера.
1 / 15 = 1/15 часть работы в час.
Находим продуктивность работы двух мастеров вместе.
1/10 + 1/15 = (Общий знаменатель 60) = 6/60 + 4/60 = 10/60 = 1/6 часть работы в час.
Находим общее время работы двух мастеров.
Для этого делим работу на продуктивность.
1 / 1/6 = 1 * 6/1 = 6 часов.
За 6 часов.