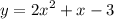
Дано:
S = 203 км - расстояние АВ.
m = 100 км/ч - скорость второго
t1 = 3 ч - время задержки второго
Найти: Sc = ? - расстояние АС.
Пошаговое объяснение:
Делаем схему движения - рисунок в приложении. n - скорость первого.
Постановка задачи: АС = m*tc = 110*tc. Найти - tc- время "погони".
Можно написать такие уравнения:
1) d = n*t1 = 3*n - дистанция "погони" - первый "убежал".
2) tc = d/(m-n) - время до встречи "погони"
3) T = S/n = 203/n - время в пути первого - прибыл в пункт В.
4) Т = 3 + 2*m*tc - одновременно - первый прибыл в пункт В, а второй вернулся в пункт А.
Пробуем составить окончательное уравнение.
5) 203/n = 3 + 2*3*n/(110-n)
203/n = 3 + 6*n/(110-n)
6) 203*(110-n) = 3*n*(110-n) + 6n²
7) 22330 - 203*n = 330*n - 3n² + 6n²
8) 3*n² - 127*n - 22330 = 0
Решаем квадратное уравнение и получаем:
D = 284089, √D = 533, и два корня: n1 = 110 и УРА - n = 67 2/3 (≈67.(6))
Дальше не решается, где-то ошибки, но может быть подсказка
Пошаговое объяснение:
Чтобы построить график берем стандартную параболу у=х²(красного цвета),х= -2, -1 , 0 , 1 , 2
у= 4, 1 , 0 , 1 , 4 и строим ее.
кроме того "сжимаем параболу" в 2 раза(у= 2х² -синяя парабола)
х= -2, -1 , 0 , 1 , 2
у= 8, 2 , 0 , 2 , 8 строим ее синим цветом.
,а затем переносим вершину на 0,5 влево и опускаем на 3,5 единицы вниз по оси у. Вершина в точке (-0,5;-3,5)
На чертеже изображена зеленым цветом данная парабола после переноса на ее место с вершиной в точке (-0,5;-3,5).
Это та же "синяя" парабола , перенесенная на -0,5 (влево) и на -3,5 единиц( вниз).
Параллельный перенос вершины в науденную точку. в решении точку.