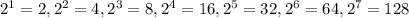и т.д.
Получаем, что двойка в степенях оканчивается на 2, 4, 8, 6, далее снова на 2, 4, 8, 6 и так до бесконечности. Используем закономерность "четвёрок" этих чисел.
32 делится на 4, значит 2 в степени 32 заканчивается цифрой 6
69 не делится на 4, зато 68 делится на 4, получаем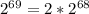 
Произведение двойки и числа, оканчивающегося на 6 равно 12, т.е. оно оканчивается на 2
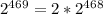468 делится на 4, значит аналогично предыдущему произведение
заканчивается цифрой 2
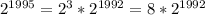
Произведение 8 и 6 равно 48, значит всё произведение заканчивается на 8
Так и объясняйте ребёнку! Успеха!
Пусть медиана исходит из вершины А к стороне ВС. Воспользуемся следующим свойством медианы: точка, в которой пересекаются все медианы - центроид - делит каждую из них в соотношении 2:1, считая с вершины. Таким образом, получаем длину отрезка АМ, где М - точка пересечения, АМ = 20 см.
Высота ВЕ, которую необходимо найти в задаче, образует прямой угол с основанием, поэтому в треугольнике АМЕ находим сторону АЕ, АЕ = 10√3. основание АС равно 2*АЕ и составляет АС = 20√3.
Теперь, с данной в условии медианы и найденного основания можно найти половину стороны ВС (медиана делит сторону пополам). Это можно сделать с теоремы косинусов, таким образом, DC = 10√3, а ВС = 2*DC = 20√3.
Основание равно боковой стороне, значит треугольник не просто равнобедренный, но равносторонний. Длину высоты можно найти, опять применив теорему косинусов, зная, что все углы в равностороннем треугольнике равны 60°, но также в подобном треугольнике все медианы равны. Высота, опущенная на основание, таким образом, будет составлять 30 см.