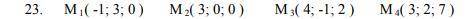
ответ: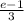
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
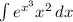Пусть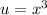 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/3966/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/3966/640b8.png)
Здесь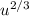 
сокращаются и мы имеем 
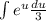. Выносим 
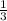за интеграл: 
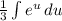. Теперь мы имеем знакомый интеграл, который равняется 
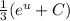, тоже самое что 
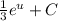. Подставляем 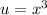и имеем 
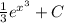. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/3966/3089c.png)
ответ: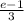
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
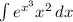Пусть 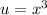, тогда .
Делаем подстановку в наше изначальное выражение:
Здесь 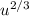сокращаются и мы имеем 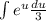. Выносим 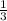за интеграл: 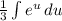. Теперь мы имеем знакомый интеграл, который равняется 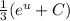, тоже самое что 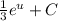. Подставляем 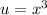и имеем 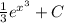. Используем фундаментальную теорему исчисления:
Геометричним вектором або просто вектором називається спрямований відрізок. Якщо А – початкова точка, а В – кінцева, то вектор позначається AB . Якщо початок і кінець вектора не вказуються, то його позначають малою буквою латинськогоалфавіту a,b,c,
Вектор BA називають протилежним вектору AB . Вектор a є протилежним вектору a .
Довжиною або модулем вектора називається відстань між його початком і кінцем. Модулі векторів AB і a позначаються відповідно AB і a . Вектор, довжина якого дорівнює одиниці, називається одиничним. Одиничний вектор
того самого напряму, що й вектор a , називають його ортом і позначають a 0 . Вектор, у якого початок і кінець збігаються, звуть нульовим вектором і
позначають як 0 . Його довжина дорівнює нулю, а напрямок не визначений.
Вектори a і b називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих a b. Нульовий вектор вважається колінеарним будь-якому іншому вектору.
Два вектори a і b називають рівними a b , якщо вони колінеарні, мають однакові довжини й однакові напрямки.
З визначення рівності векторів випливає, що вектори можна переносити паралельно самим собі, не порушуючи їх рівності. Такі вектори називаються
вільними. Вектори, які утворюються паралельним перенесенням уздовж a і лежать з ним на одній прямій називають ковзаючими векторами.