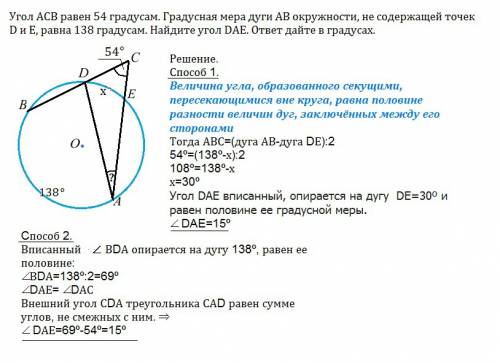
Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
(х+2)²-4+8=4у;
(х+2)²=4у-4; (х+2)²=4*(у-1);
если обозначим у-1=у₁; х+2=х₁, то перенося начало координат в точку
(х₁;у₁), получим уравнение параболы
х₁²=4у₁ - каноническое уравнение.
2р=4⇒р=2; р/2=1; фокус F(0;р/2); F(0;1)
уравнение директрисы х=-р/2, т.е. х₁=-1, уравнение директрисы в старой системе координат имеет вид х+2=-1; т.е. х=-3.
x² + 4x - 4y + 8 = 0⇒у=(х²/4)+х+2; координаты вершины
х₀=-b/2a=-1/(2*0.25)=-2; у₀=1-2+2=-1,