Question

Вычислить определители методом рекуррентных соотношений

Answer 1

Обозначим этот определитель через $D_n.$ Раскладывая его по первой строке, получаем

$D_n=3D_{n-1}-2\begin{vmatrix}1&2&0&\ldots&0&0\\0&3&2&\ldots &0&0\\0&1&3&\ldots&0&0\\\hdotsfor{6}\\0&0&0&\ldots&3&2\\0&0&0&\ldots&1&3\end{vmatrix}=3D_{n-1}-2D_{n-2}$

(последнее равенство получено с разложения по первому столбцу). Конечно, в этом равенстве предполагается, что n>2.

Непосредственно ищем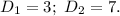 $D_1=3;\ D_2=7.$ используя выведенную формулу, находим 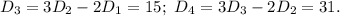$D_3=3D_2-2D_1=15;\ D_4=3D_3-2D_2=31.$ Замечаем такую закономерность:

$D_1=3=2^2-1;\ D_2=7=2^3-1;\ D_3=15=2^4-1;\ D_4=31=2^5-1.$

Естественно возникает гипотеза, что для любого натурального n

                                                   $D_n=2^{n+1}-1.$

Докажем это. Для начальных значений n гипотеза уже проверена, остается проверить индукционный переход. А именно, предположив, что гипотеза верна при n=k и n=k+1, докажем, что тогда она верна и при n=k+2. В самом деле,

$D_{k+2}=3D_{k+1}-2D_{k}=3\cdot (2^{k+2}-1)-2\cdot(2^{k+1}-1)=3\cdot 2^{k+2}-2^{k+2}-1=$

$=2\cdot 2^{k+2}-1=2^{k+3}-1.$

Тем самым гипотеза доказана при всех натуральных  n.

Замечание. Задачу можно было бы решить с характеристического уравнения, но в этом случае пришлось бы слишком много объяснять.

ответ:   $D_n=2^{n+1}-1.$