Question

Вычислить площадь фигуры,ограниченной линиями: у=х^2-4x,y=0

Answer 1

Площадь фигуры, ограниченной данными линиями

$\displaystyle S = 10\frac{2}{3}$   ед.²

Пошаговое объяснение:

Надо вычислить площадь фигуры, ограниченной линиями:

$\displaystyle y=x^2-4x;\;\;\;\;\;y=0$

1. Для того, чтобы вычислить площадь фигуры, надо построить эти графики и найти точки их пересечения:

Первый график - парабола, ветви вверх.

Второй график - это ось 0х.

Если у = 0, то

$\displaystyle x^2 - 4x = 0\\\\x(x-4)=0\\\\x_1=0;\;\;\;\;\;x_2=4$

Формулы для вычисления площади фигуры, ограниченной линиями:

$\displaystyle \boxed {S=\int\limits^a_b {(f_2(x)-f_1(x)}) \, dx}\;\;\;\;\;(1)$

также нам понадобится формула Ньютона - Лейбница:

$\displaystyle \boxed { \int\limits^a_b {f(x)} \, dx =F(a)-F(b)}\;\;\;\;\;(2)$

2. В нашем случае:

f₂(x) = 0 (ограничивает сверху);   f₁(х) = х² - 4х (ограничивает снизу);

b = 0;   a = 4.

Подставим эти значения в формулу (1) и с формулы (2) вычислим площадь фигуры:

$\displaystyle \int\limits^4_0 {(0-x^2+4x)} \, dx =\left(-\frac{x^3}{3}+4*\frac{x^2}{2}\right) \left|^4_0=\left(-\frac{4^3}{3}+2*4^2\right)-0 =$

$\displaystyle =-21\frac{1}{3}+32=10\frac{2}{3}$  (ед²)

⇒ площадь искомой фигуры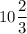   $\displaystyle 10\frac{2}{3}$  ед.²