на последнее место идет четная цифра-(0 ; 6)
два варианта
на первое любое число,кроме 0- 3 варианта
на второе по третье место можно ставить любую цифру из 4, по 4 варианта на каждое место
2×3×4×4×4= 384 вариантов
2)
Упростить уравнение,используя универсальную тригонометрическую подстановку:
;
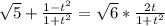Решить уравнение относительно t:
;
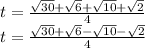Сделать обратную подстановку t=tg(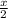
):
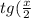)=\frac{\sqrt{30}+\sqrt{6}+\sqrt{10}+\sqrt{2}}{4}\\
tg(\frac{x}{2} )=\frac{\sqrt{30}+\sqrt{6}-\sqrt{10}-\sqrt{2}}{4} [/tex];
Решить уравнение относительно x:
x=2arctg(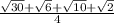
)+2kπ,k∈Z
x=2arctg(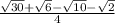
)+2kπ,k∈Z;
Поскольку универсальная замена переменной может быть использована только если x≠π+2kπ,k∈Z,то необходимо проверить является ли x=π+2kπ,k∈Z также решением уравнения:
;
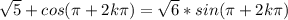Упростить выражение,используя cos(+-2*k*π)=cos(t),k∈Z:
;
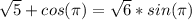Упростить равенство:
1,23607=0;
π+2kπ,k∈Z не является решением,следовательно,его не нужно добавлять:
x=2arctg(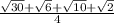)+2kπ,k∈Z
x=2arctg(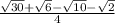)+2kπ,k∈Z;
ответ: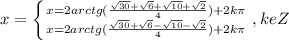
Сумма 1 + 2 + 3 + ... + n = n(n + 1)/2 = 81k
n(n + 1) = 162k
Число 162k является произведением двух последовательных чисел.
Можно разложить его на множители:
162k = 2*3^4*k = 2*81k = 3*54k = 6*27k = 9*18k = 18*9k = 27*6k = 54*3k = 81*2k
Произведения 2*81k = 3*54k = 6*27k = 9*18k очевидно, не подходят.
Возьмем 18*9k. Соседние с 18 числа 17 и 19 на 9 не делятся.
Возьмем 27*6k. Соседние с 27 числа 26 и 28 на 6 не делятся.
Возьмем 54*3k. Соседние с 54 числа 53 и 55 на 3 не делятся.
Возьмем 81*2k. Соседние с 81 числа 80 и 82 на 2 делятся.
Наименьшее n = 81, сумма равна 81*82/2 = 3321.
ответ 81.
Пошаговое объяснение:
В разряде десятков тысяч может стоять одна из трех цифр, в разряде тысяч может стоять одна из четырех цифр, в разряде сотен и десятков тоже одна из четырёх цифр, в разряде единиц одна из двух четных цифр. Итого: 3*4*4*4*2=384 числа