Поскольку при выкладывании по 13 и по 14 плиток в ряд прямоугольников не получается, а остаются неполные ряды, то количество плиток делится на 13 и на 14 с остатками.
Остаток от деления любого числа на 13 не может быть больше 12. По условию это число на 11 больше, чем остаток от деления на 14. Но остаток от деления на 14 тоже не равен нулю. Значит, остаток от деления на 13 может быть равен только 12. А остаток от деления на 14 равен 1.
Общее количество плиток меньше 100, иначе их хватило бы на квадратную площадку со стороной в 10 плиток. Среди чисел меньше 100 надо найти такое, которое делится на 13 с остатком 12 и на 14 с остатком 1. Проверив все числа в пределах 100, делящиеся на 14 с остатком 1, получим ответ: 77 плиток.
Пошаговое объяснение:
Пошаговое объяснение:
1 - это уравнение прямой в параметрической форме записи.
2 - для построения удобнее использовать каноническую форму уравнения прямой : y = k*x + b.
РЕШЕНИЕ
- 2*x +3*y - 12 =0 - дано
3*y = 2*x+ 12
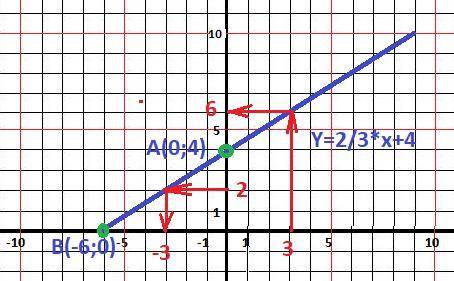
y = 2/3*x + 4 - каноническая форма уравнения прямой.
Для построения прямой достаточно знать координаты двух точек.
Первая - точка пересечения с осью ОУ - при Х = 0
y(0) = b = 4. Точка А(0;4).
Вторая - точка пересечения с осью ОХ - решаем при у = 0.
0 = 2/3*х + 4
х = - 4 /(2/3) = - 6. Точка В(-6;0)
Рисунок с графиком в приложении.
ответы на вопросы находим с графика.
1) у = 2 - ордината, х = -3 - абсцисса - ответ.
2) х = 3 - абсцисса, у = 6 - ордината - ответ.
Если к обеим частям уравнения прибавить один и тот же многочлен от, то получим уравнение, равносильное данному
Равносильные преобразования. Если к обеим частям уравнения прибавить один и тот же многочлен от, то получим уравнение, равносильное данному. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Пошаговое объяснение: