

Четырехугольник ABCD.
BE = CD = 5
(
с
м
2
)
;
1) AE * BE : 2 = 2 * 5 : 2 = 10 : 2 = 5
(
с
м
2
)
− площадь треугольника ABE;
2) ED * CD = 5 * 5 = 25
(
с
м
2
)
− площадь квадрата EBCD;
3) 5 + 25 = 30
(
с
м
2
)
− площадь четырехугольника ABCD.
ответ: 30
с
м
2
Треугольник KMNF.
1) KF * MF : 2 = 6 * 10 : 2 = 60 : 2 = 30
(
м
2
)
− площадь треугольника KMF;
2) MF * FN : 2 = 10 * 3 : 2 = 30 : 2 = 15
(
м
2
)
− площадь треугольника MFN;
3) 30 + 15 = 45
(
м
2
)
− площадь треугольника KMNF.
ответ: 45
м
2
Четырехугольник PTQR.
1) PX * TX : 2 = 5 * 8 : 2 = 40 : 2 = 20
(
д
м
2
)
− площадь треугольника PTX;
2) TX * XY = 8 * 7 = 56
(
д
м
2
)
− площадь прямоугольника TQXY;
3) QY = TX = 8 (дм);
QY * YR : 2 = 8 * 4 : 2 = 32 : 2 = 16
(
д
м
2
)
− площадь треугольника QYR;
4) 20 + 56 + 16 = 76 + 16 = 92
(
д
м
2
)
− площадь четырехугольника PTQR.
ответ: 92
д
м
2
Пошаговое объяснение:
3242
Пошаговое объяснение:
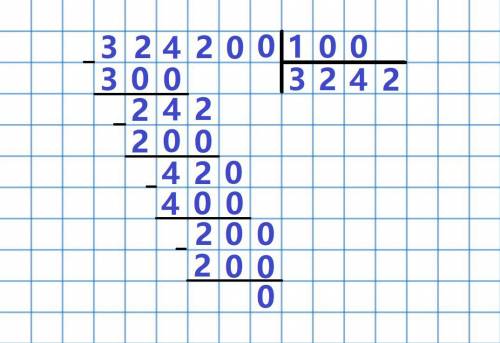
324200 : 100 = ?
1. Записываем данный пример в столбик (см вложение).
2. Выделяем первое неполное делимое и определяем кол-во цифр в частном (первое неполное частое это 324).
3. Делим 324 на 100 (324 : 100 = 3 (ост. 24)).
4. Списываем 2 сотни и делим 242 на 100 (242 : 100 = 200 (ост. 42).
5. Списываем 0 десятков и делим 420 на 100 (420 : 100 = 4 (ост. 20).
6. Списываем 0 единиц и делим 200 на 100 (200 : 100 = 2).
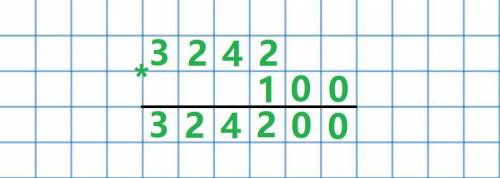
Проверка:
1. Записываем пример 3242 * 100 в столбик (см вложение).
2. Перемножаем единицу на все цифры числа 3242.
3. После вычислений добавляем к результату столько нулей, сколько стоит в числе 100, т.е. 2 нуля.
4. Число совпало с делимым нашего примера, значит пример решён правильно.
25%
20%
75%
Пошаговое объяснение:
788ой
160-100%
40-?
40*100/160=25%
250-100%
50-?
50*100/250=20%
600-100%
450-?
450*100/600=75%