Пошаговое объяснение:
Разделим эту фигуру на 2 квадрата и 1 прямоугольник:
1 Квадрат (большой) имеет стороны по 60мм
2 квадрат (маленький) имеет стороны = по 20мм
Прямоугольник имеет стороны = 30мм и 20мм.
Сейчас найдём их площади :
Площадь квадрата:
S = а²,
где а - сторона квадрата.
1) а = 60мм
2) а = 20мм
1) S = 60² = 60 * 60 = 3600 (мм²) - площадь большого квадрата
2) S = 20² = 20 * 20 = 400 (мм²) - площадь маленького квадрата
Площадь прямоугольника:
S = a * b,
где а и b стороны прямоугольника
3) S = 30 * 20 = 600 (мм²) - площадь прямоугольника
Чтобы найти площадь этой фигуры, нужно сложить площади двух квадратов и прямоугольника;
4) 3600 + 400 + 600 = 4600 (мм²) - площадь фигуры
ответ: 4600 мм²
Пошаговое объяснение:
ОДЗ
система
3+2x-x²≥0 ; -(x²-2x-3)≤0 x1,2=(2±√(4+12))/2=(2±√16)/2=(2±4)/2={-1;3}
x+1>0 ; x>-1
первое неравенство решим методом интервалов
- + -
II
-1 3
x∈[-1;3]
x>-1
⇒ ОДЗ x∈(-1;3] ⇒ целыми корнями могут быть только 0,1,2,3
подставим эти числа в уравнение
1) х=0 ; √3-3≠0; 0 не является корнем
2) x=1; √(3+2-1) - 3/√2=2-3/√2≠0; 1 не является корнем
2) x=2; √(3+4-4) - 3/√3=√3-3/√3≠0; 2 не является корнем
3) x=3; √(3+6-9)-3/2=-3/2≠0; 3 не является корнем
⇒ количество целых корней 0
Пусть Настя смогла это сделать. Разделим числа на две группы -- те, которые делятся на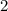
, но не делятся на 
, и те, что делятся на 
. Заметим, что в обеих группах поровну чисел, а потому они должны чередоваться на окружности. Поделим все числа на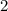 
-- получатся числа 
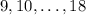. Теперь рядом стоящие числа взаимно просты, а четные и нечетные чередуются. Тогда рядом с числом 
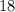должны располагаться два числа из 
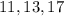(оставшиеся два нечетных делятся на 
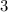), рядом с 
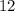тоже должны располагаться два из этих числа. Теперь можно попробовать расставить числа. Оказывается это возможно. Остается все умножить обратно на 
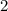и записать результат: 
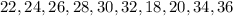(крайние тоже соседи).