
ответ: 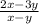
Пошаговое объяснение:
Пусть в первом пакете, весом 4кг, будет x % жирности, или же 0,01x
Пусть во втором пакете, весом 6 кг, будет y % жирности, или же 0,01y
Пусть из двух пакетов отлили одинаковое кол-во молока - k кг
1) После того, как из первого пакета отлили k кг молока, в нём осталось
4 - k кг молока;
значит масса жира первого пакета стала 0,01x·(4 - k) кг
2) После того, как из второго пакета отлили k кг молока, в нём осталось
6 - k кг молока;
значит масса жира второго пакета стала 0,01y·(6 - k) кг
3) В первый пакет добавили k кг молока из второго пакета, с массой жира 0,01y·k
Значит масса жира в первом пакете стала
0,01x·(4 - k) + 0,01y·k кг
Во второй пакет добавили k кг молока из первого пакета, с массой жира 0,01x·k
Значит масса жира во втором пакете стала
0,01y·(6 - k) + 0,01x·k кг
4) По условию жирность в двух пакетах стала одинаковой, значит можем составить уравнение:
0,01x·(4 - k) + 0,01y·k = 0,01y·(6 - k) + 0,01x·k | ×100
4x - xk + yk = 6y - yk + xk
4x - 6y = 2xk - 2yk
2x - 3y = k(x - y)
k = 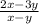
<M=140
ΔACM:
AM=CM. <CAM=<ACM=(180-140)/2, <ACM=<CAM=20
ΔACB: <BAC=60-20, <BAC=40. =>
ΔACB -равнобедренный. АС=ВС. <ACB=120-20. <ACB=100
по теореме косинусов:
АВ²=АС²+ВС²-2*АВ*ВС*cos<ACB. AC=BC=x
10²=x²+x²-2*x*x*cos100
100=2x²-2x² *cos100, 100=x²(2-2cos100)
x²=100/(2-2cos100). x²=50/(1-cos100)
BC=5√(2/(1-cos100))
ΔACM по теореме косинусов:
АС²=АМ²+СМ²-2*АМ*СМ*cos140. AM=CM=y
AC²=y²+y²-2y*y* cos140
AC²=2y²-2y²cos140. AC²=y²(2-2cos140).
y²=AC²/(2-2cos140). y²=AC²/(2(1-cos140))
y²=(50/(1-cos100))/(2(1-cos140)
y²=25/ [ (1-cos100)*(1-cos140)]
y=5/√[ (1-cos100)*(1-cos140)], CM=5/ √[(1-cos100)*(1-cos140)]
BC+CM=5√(2/(1-cos100))+5/√[ (1-cos100)*(1-cos140)]