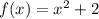 определена на множестве E
определена на множестве E 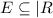
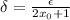 где
где 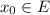 .
. на области
на области 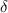 от
от  (то есть:
(то есть: 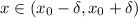 ) выполняется
) выполняется 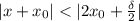 .
.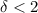 , выполняется
, выполняется 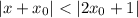 .
.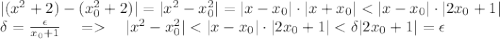
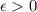 есть
есть 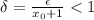 , на области которой выполняется
, на области которой выполняется 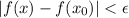
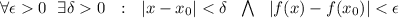 ). Следовательно -
). Следовательно - 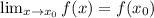 .
.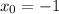 нужно отдельно доказать предел
нужно отдельно доказать предел 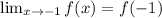 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 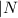 тоже подмножество
тоже подмножество  , значит
, значит 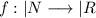 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 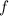 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 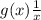 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 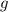 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 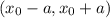 "...
"...
переведем минуты в секунды:
3 мин 24 с = 180+24= 204
4 мин 3 с = 240+3= 243
2 м = 120
1) 204+243+120= 567 с - всего
2) 567 : на кол-во данных ( 3 ) = 189 с
переведем в первоначальный вид - 3 минуты и 9 секунд.
ответ: среднее время прохождения - 3 минуты 9 секунд.
Пошаговое объяснение:
удачи,надеюсь !:)