4/52 = 1/13 - вероятность выбрать взять карту «короля»
теперь надо расписать все возможные варианты для 5 карт
К - король; Х - не король:
вообще в данном случае много вариантов, поэтому я напишу только один вариант, который не подходит, ведь только при одном варианте королей вообще не будет: Х Х Х Х Х
вероятность этого события надо вычислить и вычесть и 1 (100%)
вероятность достать карту не с королем = 1 - 1/13 = 12/13
так как мы достаем 5 карт, то вероятность (Х Х Х Х Х) =
1)f(x)=log5(x-6/x^2+3x) ОДЗ: (x-6)/(x^2+3x) >0 Определим, при каких значениях Х выражения, стоящие в числителе и знаменателе, обращаются в нуль: x-6=0; x=6 x^2+3x=0; x(x+3)=0; x=0 U x=-3 Нанесем эти числа на числовую ось: -(-3)+(0)-(6)+
ответ: D(y)= (-3;0) U (6; + беск.)
2)V - знак корня V(15x^2-x+12)=4x ОДЗ: x>=0 Возведем обе части уравнения в квадрат: 15x^2-x+12=16x^2 15x^2-x+12-16x^2=0 -x^2-x+12=0 x^2+x-12=0 D=1^2-4*1*(-12)=49 x1=(-1-7)/2=-4 - посторонний корень x2=(-1+7)/2=3 ответ: 3
3)2cos^2x-5cos x-7=0 Замена: cosx=t, -1<=t<=1 2t^2-5t-7=0 D=(-5)^2-4*2*(-7)=81 t1=(5-9)/4=-1 t2=(5+9)/4=3,5 - посторонний корень Обратная замена: cos x=-1 x=П + 2Пк, k e Z
0,33
Пошаговое объяснение:
4/52 = 1/13 - вероятность выбрать взять карту «короля»
теперь надо расписать все возможные варианты для 5 карт
К - король; Х - не король:
вообще в данном случае много вариантов, поэтому я напишу только один вариант, который не подходит, ведь только при одном варианте королей вообще не будет: Х Х Х Х Х
вероятность этого события надо вычислить и вычесть и 1 (100%)
вероятность достать карту не с королем = 1 - 1/13 = 12/13
так как мы достаем 5 карт, то вероятность (Х Х Х Х Х) =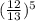
что примерно равняется 0,67
теперь из 100% вычитаем полученные 67%
1 - 0,67 = 0,33