х-скорость первого;
у-скорость второго;
Необходимо составить систему уравнений первым уравнением будет:
3⅓(х+у)=30;
по второй части условия видно что первый бы шел 4,5 часа, а второй 2,5 следовательно получаем уравнение:
4,5х+2,5у=30
домножим первое уравнение на 3 получим:
10х+10у=90;
домножим второе уравнение на 2, получим:
9х+5у=60;
домножим второе уравнение на 2 и выразим оттуда 10у:
10у=120-18х;
подставим 10у в первое уравнение, откуда находим: х=3,75
далее подставляем значение х в любое уравнение и получаем у=5,25
h = √51 + √149 ≈ 19,3 м
h = √149 - √51 ≈ 5 м
Пошаговое объяснение:
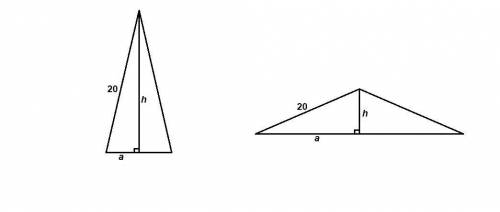
Высота равнобедренного треугольника, проведенная к основанию, является медианой.
Обозначим высоту h, половину основания а.
Площадь треугольника равна половине произведения основания на высоту:
S = ah,
по теореме Пифагора составим второе уравнение:
a² + h² = 400
Получаем систему уравнений:
ah = 98 (1)
a² + h² = 400
Домножим первое уравнение на 2 и вычтем из второго:
2ah = 196
a² - 2ah + h² = 204 (2)
2) (a - h)² = 204
|a - h| = √204
|a - h| = 2√51
Возможны два случая:
1. a < h
h - a = 2√51
a = h - 2√51
Подставим выражение в (1):
h² - 2√51h - 98 = 0
D/4 = 51 + 98 = 149
h = √51 - √149 - не подходит по смыслу задачи
h = √51 + √149 ≈ 19,3 м
2. a > h
a - h = 2√51
a = h + 2√51
Подставим в (1):
h² + 2√51h - 98 = 0
D/4 = 51 + 98 = 149
h = - √51 - √149 - не подходит по смыслу задачи
h = - √51 + √149 = √149 - √51 ≈ 5 м
____________________________________________
Применена формула сокращенного дискриминанта при решении квадратного уравнения:
ax² + bx + c = 0
D/4 = (b/2)² - ac
x = (- b/2 ± √(D/4)) / a
r^3+15r^2+75r+125
Пошаговое объяснение:
r^3+3r^2×5+3r×25+125
r^3+15r^2+75r+125