Question

Я вывел свойство, что если корни функций f(x) и g(x) такие, что $f(x) : x_{1}, x_{2}, ..., x_{n-1}, x_{n}$

Тогда корни производных этих функции также относят как k


Я доказал это для квадратичных и кубических функций. Вопрос: можно ли доказать это свойство в общем виде для произвольных функций m-ой степени

$g(x) : kx_{1}, kx{2}, ..., kx{n-1}, kx_{n}$
$f'(x) : x_{'1}, x_{'2}, ... , x_{'n-1}, x_{'n}\\g'(x) : kx_{'1},k x_{'2}, ... , kx_{'n-1}, kx_{'n}\\$

Answer 1

Сформулируем условие более четко:

Определим для $\forall n\in N, n\geq 2,\;\forall k\neq 0$ функции   $f(x)=(x-x_1)\cdot ...\cdot (x-x_n),g(x)=(x-kx_1)\cdot ...\cdot (x-kx_n)$. Требуется доказать, что, если производная 1ой функции $f'(x)=(x-x'_1)\cdot ...\cdot (x-x'_{n-1})$, то производная 2ой имеет вид $g'(x)=(x-kx'_1)\cdot ...\cdot (x-kx'_{n-1})$.

Пошаговое объяснение:

Заметим, что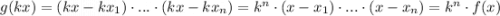 $g(kx)=(kx-kx_1)\cdot ...\cdot (kx-kx_n)=k^n\cdot (x-x_1)\cdot ...\cdot (x-x_n)=k^n\cdot f(x)$.

Продифференцировав, получим:

$g'(kx)\cdot k=k^n\cdot f'(x)$

Подставив в него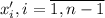 $x'_i,i=\overline{1,n-1}$, получим

$g'(kx'_i)=k^{n-1}\cdot \underbrace{f'(x'_i)}_0\Rightarrow g'(kx'_i)=0$

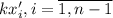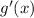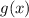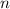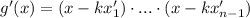Т.е. в $n-1$ точке $kx'_i,i=\overline{1,n-1}$ многочлен $n-1$ степени $g'(x)$ [т.к. по условию степень $g(x)$ равна $n$] обращается в 0 - это и означает, что $g'(x)=(x-kx'_1)\cdot ...\cdot (x-kx'_{n-1})$.