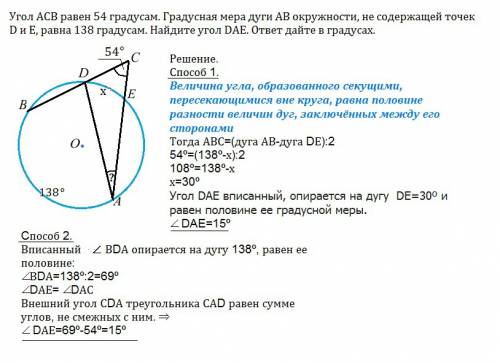
Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
а) 12.
d) Так как нет больше никаких дополнительных условий (неотрицательность значений и т.п.), то возможны два ответа -16; 45.
с) 20.
Пошаговое объяснение:
а) 3,6, ___, 17, 20, 26
Найдем среднее арифметическое. Им будет (3+6+17+20+26+х)/6. По условию оно равно 14. Составим уравнение:
(3+6+17+20+26+х)/6=14
72+х=14*6
72+х=84
х=84-72
х=12 - пропущено.
d) Размах равен разности между самым большим и самым маленьким числом. Самым большим будет 26. Самым маленьким 3. 26-3=23. Тут требуется, чтобы было 42.
Значит самым маленьким числом может быть 26-42=-16.
Возможен другой вариант 3+42=45.
Так как нет требований, чтобы число было неотрицательным, то возможно два ответа: -16 и 45.
с) Мода равна числу, которое наиболее часто встречается. Тут все числа встречаются по одному разу. Чтобы мода была равна 20. Надо вместо пропущенного числа вставить 20. Значит тогда чисел 20 будет две штуки. Поэтому в данном случае пропущенное число равно 20.
покажи Кординат