9;-9
Пошаговое объяснение:
т.к модуль это расстояние от точки начало отсчета,до точки на прямой,поэтому он не может быть выражен отрицательным числом.
во втором случае уравнение не имеет корней
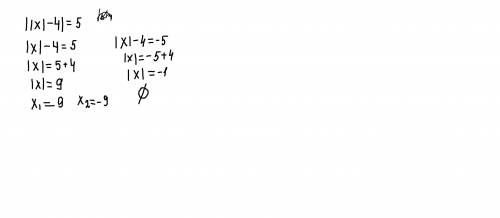
Решение 1. Вместо суммарного процента будем считать суммарную долю девочек ― очевидно, эти числа отличаются в 100 раз и достигают своего максимума одновременно. Каждая девочка в классе из 22 человек составляет от общего числа учащихся в этом классе, а в классе из 23 человек ― от общего числа учащихся. Значит, если поменять местами девочку из большего класса и мальчика из меньшего, суммарный процент девочек вырастет. Таким образом, максимум достигается, когда все подобные перестановки сделаны, то есть, когда меньший класс полностью состоит из девочек, а в большем классе ― 3 девочки и 20 мальчиков.
Решение 2. Пусть в меньший класс распределено х девочек (где ), тогда в больший класс попало девочек. Значит, суммарная доля девочек в двух классах равна и представляет собой линейную функцию с положительным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на правом конце промежутка [2; 22], то есть при Таким образом, меньший класс полностью должен состоять из девочек, а в большем классе должно быть 3 девочки и 20 мальчиков.
ответ: В одном классе ― 22 девочки, в другом ― 3 девочки и 20 мальчиков.
ответ: Р=32 см.
Пошаговое объяснение:
"диагонали параллелограмма равны 14 и 8 см а стороны относятся как 9: 7. Найдите периметр параллелограмма".
***
АВСВ- параллелограмм. АС=14 см, BD=8 см - диагонали параллелограмма. АВ и ВС - стороны.
Пусть меньшая сторона параллелограмма равна 7х. Тогда большая равна 9х.
По свойству параллелограмма:
АС²+BD²=2(AB²+BC²);
14²+8²=2((7x)²+(9x)²);
(196+64)/2=49x²+81x²;
130=130x²;
x²=1;
x=±1; (-1 - не соответствует условию).
Меньшая сторона равна 7х=7*1=7 см.
Большая сторона равна 9х=9*1=9 см.
Р ABCD=2(a+b), где a и b - стороны параллелограмма
Р=2(7+9)=2*16=32 см.
Пошаговое объяснение:
Х1= 9
Х2= -9