ответ: а) 30, б) 3
Указание. Пусть в первом контейнере находится x коробок массой 19 кг и y коробок массой 49 кг. Тогда во втором контейнере находится соответственно 25-x и 19-y коробок. Тогда модуль разности суммарной массы можно записать: S=|19x+49y-((33-x)∙19+(27-y)∙49)| или S=2∙|19x+49y-975|.
a) Требование равенства количества коробок дает дополнительное условие x+y=30, поэтому выражение для модуля разности запишется S=2∙|19x+1470-49x-975|=
2*I495-30xI=30∙|33-2x|. Поскольку xϵZ, то минимальное значение модуля разности может быть сделано равным только единице |33-2x|>=1, поэтому ответ на п.а) 30.
б) Нужно найти количество коробок массы которых будут приблизительно одинаковыми:
49 кг * 2 кор.=98 кг
19 кг * 5 кор.=95 кг
98-95=3 кг
наименьшее значение S= 3
упрощаем выражение, получаем y=x^3-25*x^2-208*x-586, возьмем первую производную от данного выражения:
y'=3x^2-50x-208, исследуем поведение функции, найдем нули производной получаем 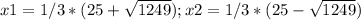
Это парабола, ветви направлены ввех, т.к коэффициент перед х^2>0, значит она меньше нуля на промежутке (х2;х1)
Промежуток (2.8;5) включен в промежуток (х2;х1), значит на нем функция y=x^3-25*x^2-208*x-586 убывает, т.к производная <0. Если функция убывает то наибольшее значение функции будет достигаться на границе промежутка.
Т.к. в задаче речь идет о промежутке, а не об отрезке, то нельзя найти строгое решение задачи, только предел.
Будем предполагать что речь идет об отрезке [2.8;5].
Подставим х=2.8 в исходное выражение и получим -177. 648
ответ: наибольшее значение достигается при х=2.8 и равно -177.648
P.S. я указал только метод решения, сами вычисления лучше проверить.
Пошаговое объяснение:
Не может быть только треугольником, см. рисунок:
Если цилиндр стоит вертикально, то его проекцией будет круг.
Если цилиндр лежит горизонтально, то его проекцией будет либо прямоугольник (если длина больше диаметра основания), либо квадратом (если длина равна диаметру основания).
А треугольником, да еще и равнобедренным как ни крути - не выйдет.