-8 +11(X) + (X) + 3 = 4 (X) - 1
-5 + 12 (X) = 4(X) - 1
12(x) - 4(X) =-1 +5
8(X) =4
(X) = 4:8
(X) = 0,5 или 1/2
x1 = 0,5 или 1/2
X2 =-0,5 или 1/2
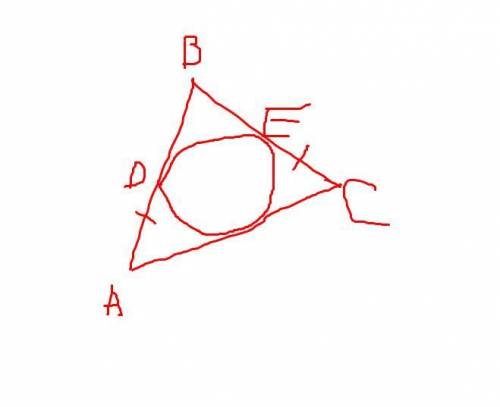
Чертеж с тем, что нам дано изначально, в прикрепленных файлах.
По условию дано, что AD=EC. Интересующие нас стороны - это AB и BC. Равные по условию отрезки являются их частями => AB-BD=BC-BE.
Поэтому для доказательства равенства AB и BC нам нужно лишь доказать равенство отрезков BD и BE.
AB и BC треугольника ABC являются двумя касательными к окружности, причем из 1 точки B. Применяем свойство двух касательных к окружности из 1 точки: Если две касательные к одной окружности исходят из 1 точки, то равны отрезки из этой точки до самой окружности. BD и BE - это отрезки из B до окружности => они равны.
Пошаговое объяснение:
-8 + 11|х| + |х| + 3 = 4|х| - 1
-5 + 12|х| = 4|х| - 1
12|х| - 4|х| = -1 + 5
8|х| = 4
|х| = 4 : 8
|х| = 0,5 или 1/2
х1 = 0,5 или 1/2
х2 = -0,5 или -1/2