Сначала интересная теория:
Область определения D(f) функции f(x) - это все те значения "x", которые можно подставить в функцию. И при этом она будет иметь смысл, то есть вычисляться.
В данном примере - функция дробная. Значит, знаменатель не должен равняться нулю. Решаем:
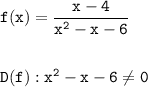
Составим и решим уравнение:
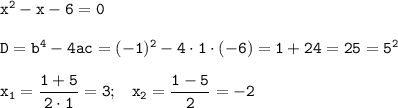
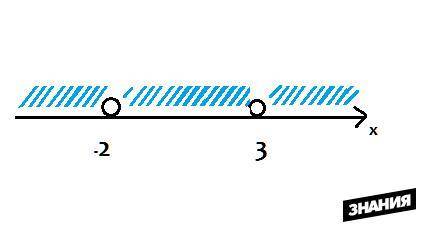
теперь чертим числовую прямую и отмечаем область значений, картинка в приложении. Точки -2, 3 выколотые, так как их нельзя подставлять в функцию: при них знаменатель обращается в ноль
D(f) = (-∞;-2)⋃(-2;3)⋃(3;+∞)
ответ: D(f) = (-∞;-2)⋃(-2;3)⋃(3;+∞)
36 | 2 48 | 2 60 | 2
18 | 2 24 | 2 30 | 2
9 | 3 12 | 2 15 | 3
3 | 3 6 | 2 5 | 5
1 3 | 3 1
36 = 2² · 3² 1 60 = 2² · 3 · 5
48 = 2⁴ · 3
НОК = 2⁴ · 3² · 5 = 720 - наименьшее общее кратное
720 : 36 = 20 брусков пл 36 см
720 : 48 = 15 брусков по 48 см
720 : 60 = 12 брусков по 60 см
ответ: 720 см - наименьшая длина заготовки.