Пошаговое объяснение:
Нужно составить всевозможные пары (числитель–знаменатель), состоящие из элементов множества, где первое число меньше второго (все данные отношения меньше 1), всего 21 вариант. После сокращения каждой из дробей сравнить с приведенными отношениями, выбрать правильные соотношения.
1) С числителем 12: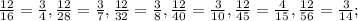 
2) С числителем 16: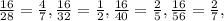 
дробь 
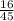несократима;
3) С числителем 28: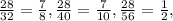 
дробь 
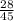несократима;
4) С числителем 32: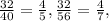 
дробь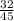 
несократима;
5) С числителем 40: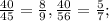 
6) С числителем 45: дробь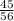 
несократима.
Таким образом, отношение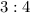 
дают пара 12–16; 
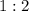— пары 16–32 и 28–56; 
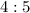— пара 32–40; 
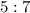— пара 40–56; 
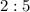— пара 16–40; 
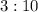— пара 12–40.
ответ: 4) n(m - n); 5) xy(x - y); 6) 2mn(3 + 4mn);
7) -y(x + y); 8) 6n(m - 2n); 9)-4x²y²(1 - 4xy).
Пошаговое объяснение:
Это примеры на вынесение за скобки общего множителя, т.е. смотрим на выражение и выбираем, какие одинаковые множители есть в каждом из одночленов, входящих в выражение. Их выносим за скобки (как бы "делим" на них), а в скобках записываем те множители, которые остануться после "деления".
Поэтому:
4) mn - n² = n(m - n);
5) x²y - xy² = xy(x - y);
6) 6mn + 8m²n² = 2mn(3 + 4mn);
7) -xy - y² = -y(x + y);
8) 6mn - 12n² = 6n(m - 2n);
9) -4x²y² + 16x³y³ = -4x²y²(1 - 4xy).
Пошаговое объяснение:
четверть не указана