ответ: 210 вариантов - чисел.
В этих числах цифры должны идти на уменьшение.
Сначала все 10 цифр расположим так: 9876543210.
По условию задачи надо получить четырёхзначное число - нужно оставить 4 или вычеркнуть 6 в любом месте из 10.
Получаем число комбинаций (сочетаний) 4-х из 10.
Вместо формулы сочетаний вида
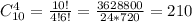
предлагаю использовать другую.
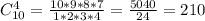
Мне нравится такая формула вычисления числа сочетаний. В числителе четыре от 10 на убывание, а в знаменателе - четыре числа от 1 на возрастание.
Для быстрого нахождения числа сочетаний в самых разных комбинациях можно применить "треугольник Паскаля". Его не трудно составить и самому. На рисунке в приложении - треугольник до 12-ой степени.

Пошаговое объяснение:
x ^ 3 - 3 * x ^ 2 + 2 = 0 ;
( x - 1 ) * ( x ^ 2 - 2 * x - 2 ) = 0 ;
1 ) x - 1 = 0 ;
Известные значения переносим на одну сторону, а неизвестные на другую сторону. При переносе значений, их знаки меняются на противоположный знак. То есть получаем:
x = 0 + 1 ;
x = 1 ;
2 ) x ^ 2 - 2 * x - 2 = 0 ;
Найдем дискриминант квадратного уравнения:
D = b ^ 2 - 4ac = (-2) ^ 2 - 4·1·(-2) = 4 + 8 = 12;
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = ( 2 - √12 ) / ( 2·1 ) = 1 - √3 ≈ -0.732;
x2 = ( 2 + √12) / ( 2·1 ) = 1 + √3 ≈ 2.732;
ответ: х = 1, х = 1 - √3 и х = 1 + √3.