В треугольнике ABC A(3; 4 ) В(2;1) С(5;2) составьте уравнения: 1) стороны BC 2) высоты, опущенной из вершины Aна сторону BC 3) медианы, проведенной из вершины C .
1. Для нахождения уравнения стороны ВС воспользуемся уравнением прямой, проходящей через две точки и :
Эти две точки: и . Получим:
2. Высота АН является перпендикулярной к прямой ВС. Угловые коэффициенты перпендикулярных прямых являются обратными противоположными числами. Так как , то . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:
Точка , угловой коэффициент . Получим:
3. Найдем середину М отрезка АВ. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка:
Вновь воспользуемся уравнением прямой, проходящей через две точки: и .
Приведите дроби к наименьшему общему знаменателю: ж)7/60,13/540 и 9/20; Можно по наибольшему из знаменателей попробовать делиться на другие или нет, если делиться то это наименьший общий будет.
540:60= 9 540:20=27
13/540 остается так 7/60= (7•9)/(60•9)= 63/540 9/20= (9•27)/(20•27)= 243/540
ответ: 63/540; 13/540; 243/540
з)52/105;7/95 и 61/63 Ищем НОК чисел 105 105|5 21|3 3|3 1|1 105=5•3•3
Приведите дроби к наименьшему общему знаменателю: ж)7/60,13/540 и 9/20; Можно по наибольшему из знаменателей попробовать делиться на другие или нет, если делиться то это наименьший общий будет.
540:60= 9 540:20=27
13/540 остается так 7/60= (7•9)/(60•9)= 63/540 9/20= (9•27)/(20•27)= 243/540
ответ: 63/540; 13/540; 243/540
з)52/105;7/95 и 61/63 Ищем НОК чисел 105 105|5 21|3 3|3 1|1 105=5•3•3
1. Для нахождения уравнения стороны ВС воспользуемся уравнением прямой, проходящей через две точки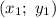 и
и 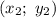 :
:
Эти две точки: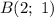 и
и 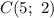 . Получим:
. Получим:
2. Высота АН является перпендикулярной к прямой ВС. Угловые коэффициенты перпендикулярных прямых являются обратными противоположными числами. Так как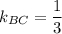 , то
, то 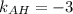 . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:
. Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:
Точка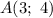 , угловой коэффициент
, угловой коэффициент 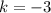 . Получим:
. Получим:
3. Найдем середину М отрезка АВ. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка:
Вновь воспользуемся уравнением прямой, проходящей через две точки: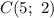 и
и 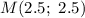 .
.
Получим: