Question

II рівень В групі спортсменів 15 курсантів з першого, 10 курсантів з другого і

5 - третього факультетів. Ймовірність виконання кваліфікаційної

норми такі: курсант першого 0,87, курсант другого - 0,76 і

курсант третього факультету - 0,74. Визначити ймовірність того, що

навмання взятий спортсмен виконає кваліфікаційну норму.

-

500

Answer 1

вероятность того, что наугад взятый спортсмен выполнит квалификационную норму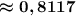  $\boldsymbol {\approx 0,8117}$

Пошаговое объяснение:

Уравнение полной вероятности.

Всего курсантов (15+10+5) = 30

Гипотезы и их вероятности (вероятности вычисляем по классическому определению вероятности P=m/n)

Н₁ = {выбран курсант 1 факультета}

P(H₁) = 15/30

Н₂ = {выбран курсант 2 факультета}

P(H₂) = 10/30

Н₃ = {выбран курсант 3 факультета}

P(H₃) = 5/30

Событие А = {наугад взятый спортсмен выполнит rвалификационную норму }

Условные вероятности нам даны в описании задачи

P(A|H₁) = 0,87

P(A|H₂) = 0,76

P(A|H₃) = 0,74

Формула полной вероятности

P(A) = P(H₁)*P(A|H₁) + P(H₂)*P(A|H₂)  + P(H₃)*P(A|H₃)

Подставим наши данные

$\displaystyle P(A) = \frac{15}{30} *0,87\,+\,\frac{10}{30} *0,76\,+\,\frac{5}{30} *0,74=$

$\displaystyle = \frac{1}{30} \bigg(15*0,87\,+\,10*0,76\,+\,5*0,74\bigg)=\frac{1}{30} *24,35=0,811(6)\approx 0,8117$

Таким образом, вероятность того, что наугад взятый спортсмен выполнит квалификационную норму  ≈ 0,8117