Question

До іть,будь ласка,з роботою по вищій математиці. Знайти похідну

Answer 1

1.   $\displaystyle y'=\frac{12}{5\sqrt[5]{x^2} } +\frac{12}{x^3} -\frac{1}{\sqrt{x} } +2$

2.   $y'=3^x(8x^3-5+2x^4\;ln\;3-5x\;ln\;3)$

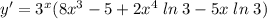
Пошаговое объяснение:

Найти производную:

1.   $\displaystyle y=4\sqrt[5]{x^3}-\frac{6x+2\sqrt{x^7} }{x^3} +2x-3$

2.   $\displaystyle y=(2x^4-5x)\cdot 3^x$

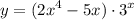
Производная суммы равна сумме производных.Формула:  $\displaystyle\bf (x^n)'=nx^{n-1}$

1. Преобразуем данное выражение:

$\displaystyle y=4\sqrt[5]{x^3}-\frac{6x+2\sqrt{x^7} }{x^3} +2x-3==4x^{\frac{3}{5} }-6x^{-2}-2x^{\frac{1}{2} }+2x-3$

Производная равна:

$\displaystyle y'=4\cdot \frac{3}{5}x^{-\frac{2}{5} } -6\cdot (-2)x^{-3}-2\cdot \frac{1}{2}x^{-\frac{1}{2} }+2-0=\\ \\=\frac{12}{5\sqrt[5]{x^2} } +\frac{12}{x^3} -\frac{1}{\sqrt{x} } +2$

Производная произведения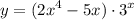: $\displaystyle\bf (uv)'=u'v+uv'$ ;  $\displaystyle \bf (a^x)'=a^x\cdot ln\;a$

2. $\displaystyle y=(2x^4-5x)\cdot 3^x$

Производная равна:

$\displaystyle y'=(2x^4-5x)'\cdot 3^x+(2x^4-5x)\cdot (3^x)'=\\ \\= (2\cdot4x^3-5)\cdot 3^x+(2x^4-5x)\cdot 3^x\cdot ln\;3==3^x(8x^3-5+2x^4\;ln\;3-5x\;ln\;3)$