В решении.
Пошаговое объяснение:
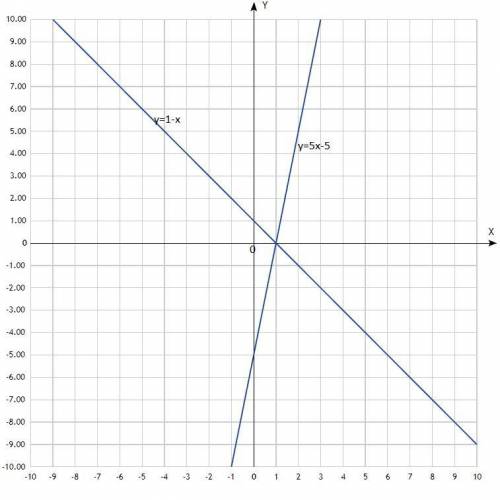
4. Решите систему уравнений графическим :
{x+y=1
{5x-y=5
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
x + y = 1 5x - y = 5
у = 1 - х -у = 5 - 5х
у = 5х - 5
Таблицы:
х -1 0 1 х -1 0 1
у 2 1 0 у -10 -5 0
Согласно графиков, координаты точки их пересечения: (1; 0).
Решение системы уравнений: (1; 0).
В решении.
Пошаговое объяснение:
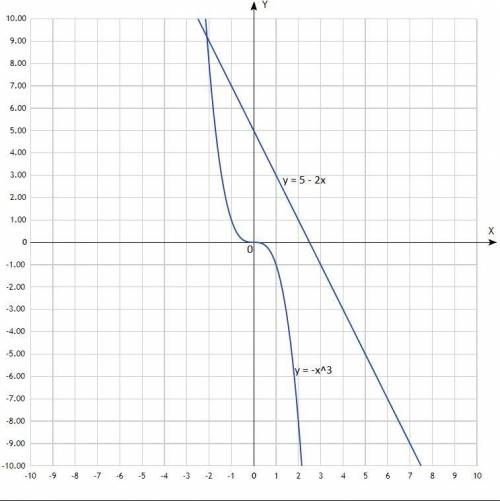
Решить графически систему уравнений:
у = -х³
2х + у = 5
Преобразовать второе уравнение в уравнение функции:
2х + у = 5
у = 5 - 2х
Построить графики функций. Первое уравнение - кубическая парабола, второе - прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -х³
Таблица:
х -2 -1 0 1 2
у 8 1 0 -1 -8
у = 5 - 2х
Таблица:
х -1 0 1
у 7 5 3
Согласно графиков, координаты точки их пересечения: (-2,1; 9,2).
Решение системы уравнений: (-2,1; 9,2).
1. Сума z₁ + z₂:
z₁ + z₂ = (8 + 3i) + (-5 + 2i) = (8 - 5) + (3 + 2)i = 3 + 5i.
2. Добуток z₁z₂:
z₁z₂ = (8 + 3i)(-5 + 2i) = -40 - 16i + 15i + 6i² = -40 - i + 6(-1) = -40 - i - 6 = -46 - i.
3. Частка z₁/z₂:
Щоб обчислити частку, спочатку виконаємо операцію множення числа z₁ на комплексно спряжене до числа z₂, а потім поділимо отримане число на квадрат модуля числа z₂.
z₁/z₂ = (8 + 3i)/(-5 + 2i) = (8 + 3i)(-5 - 2i)/((-5 + 2i)(-5 - 2i)) = (-46 - 59i)/29 = (-46/29) - (59/29)i.