См. Пошаговое объяснение
Пошаговое объяснение:
1) При линейки и карандаша построим треугольник QRS - любой, какой нам нравится. Допустим, так: слева Q, правее вверх - вершина R и ещё правее - S.
2) Ниже начинаем строить точно такой же треугольник, только вместо Q первая вершина в этом треугольнике будет называться А:
а) проводим линию;
б) на линии в любом месте отмечаем точку; называем её А;
в) в первом треугольнике циркулем измеряем длину стороны QR;
г) из точки А циркулем чертим дугу, длина которой равна QR;
д) в первом треугольнике циркулем измеряем длину стороны QS;
е) из точки А циркулем чертим дугу, длина которой равна QS; там, где эта дуга, пересечётся с линией, поставим точку; обозначим её S₁;
ж) в первом треугольнике циркулем измеряем длину стороны RS;
з) из точки S₁ циркулем чертим дугу, длина которой равна RS; эта дуга должна пересечься с первой дугой, длина которой равна QR; точку пересечения дуг обозначим В;
и) соединяем линиями построенные точки A, В и S₁ - получился треугольник AВS₁, который один-в-один должен быть такой же, как и треугольник QRS;
к) осталось построить АС; надо, чтобы АС была равна половине QS;
л) в треугольнике AВS₁ сторона AS₁ = QS, поэтому делим её пополам и отмечаем эту середину С;
м) соединяем точки АВС - построение выполнено.
ПРИМЕЧАНИЕ к пункту л):
Как при циркуля и линейки разделить отрезок пополам?
Из концов отрезка проводим 4 дуги - 2 сверху отрезка и 2 снизу отрезка; главное - чтобы эти дуги пересеклись сверху и снизу; к точкам пересечения дуг прикладываем линейку и проводим линию, пересекающую отрезок; точка пересечения - это и есть середина отрезка.
1017:
1)представим в виде двойного неравенства:
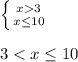
6; 7; 8,7 ( эти числа являются решениями неравенств)
2)представим в виде двойного неравенства:
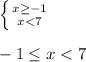
-0,5; 3; 6 (эти числа являются решениями неравенств)
3)представим в виде двойного неравенства:
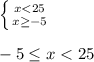
-4; -0,5; 3; 6; 7; 8,7; 15 (эти числа являются решениями неравенств)
4)представим в виде двойного неравенства:
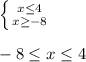
-4; -0,5; 3 (эти числа являются решениями неравенств)
============================================================
1018:
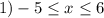
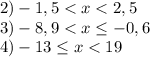
============================================================
1019:
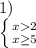
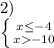
Пошаговое объяснение:
Чтобы пятизначное число было кратно 15 оно должно делиться нацело на 3 и на 5. Признаком делимости на 5 – последняя цифра 5 или 0. А признак делимости на 3 – сумма цифр кратна 3. Исходя из этих правил, подберем пятизначное кратное 15 и с двумя соседними цифрами, отличающимися на 2. Например, такое. Возьмем последнюю цифру 5, предпоследнюю 7 (отличаются на 2), а оставшиеся три выберем так, чтобы сумма цифр была кратна 3:
abc75
Цифры 7+5 = 12 – кратны 3. А другие цифры возьмем следующими: a=1, b = 3, c = 5. Получаем пятизначное:
13575
кратно 15 и любые две цифры отличаются на 2.
ответ: 13575