1.найдем пределы интегрирования, для чего определим точки пересечения графиков функций y=x² и y=4x
x²=4x; x² - 4x=0; x(x-4)=0; x=0; x=4;
2. найдем определенный интеграл от разности 4х и x², он равен
( 4*х²/2-х³/3) в пределах от нуля до 4
Используя формулу Ньютона -Лейбница, найдем площадь фигуры.
4*4²/2-4*4³/3-0=32-64/3=96/3-64/3=32/3=
10 целых и 2/3 /ед. кв./
Пошаговое объяснение:
Весь пирог = х
1-ый друг = 1/6х
2-ой друг = 1/5 * (х - 1/6х) = 1/5 * 5/6х = 1/6х
3-ий друг = 1/4 * (х - 1/6х - 1/6х) = 1/4 * 4/6х = 1/6х
4-ый друг = 1/4 * (х - 1/6х - 1/6х - 1/6х) = 1/4 * 3/6х =
3/24х = 1/8х
х - (1/6х + 1/6х + 1/6х + 1/8х) =
х - (4/24х + 4/24х + 4/24х + 3/24) =
х - 15/24х = 9/24х = 3/8х - осталось после того как угостил 4 друзей
3/8 * 1/2 = 3/16 - досталось 5-ому другу и имениннику.
1/6 + 1/6 + 1/6 + 1/8 + 3/16 + 3/16 =
8/48 + 8/48 + 8/48 + 6/48 + 9/48 + 9/48 =
48/48 = 1
Точки экстремума:
x max = 1
x min = 5
Пошаговое объяснение:
Функция
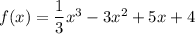
Производная функции
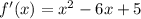
Решаем уравнение
х² - 6х + 5 = 0
D = 36 - 20 = 16 = 4²
x₁ = 0.5 (6 - 4) = 1
x₂ = 0.5 (6 + 4) = 5
График производной заданной функции - парабола веточками вверх, при х ∈ (-∞; 1] ∪ [5; + ∞) производная f'(x) > 0, а на интервале x ∈ [1; 5] f'(x) <0. Поэтому в точке x₁ = 1 знак производной меняется с + на -, то есть в точке x₁ = 1 находится максимум функции. А в точке x₂ = 5 производная меняет знак с - на +, поэтому точка x₂ = 5 - точка минимума.
Пошаговое объяснение:
найдем точки пересечения
y=x^2 и y=4x
x²=4x; x²-4x=0; x(x-4)=0; x=0; x=4; y(4)=4*4=16
₄
SOAB=SОАС-SOBAC=16*4/2-∫x²dx=
₄ ⁰
=32-(x³/3)=32-(64/3)=(96-64)/3=32/3=10 2/3 кв.ед
⁰