Находим частные производные:
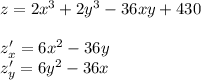
Приравниваем их к нулю и решаем систему:
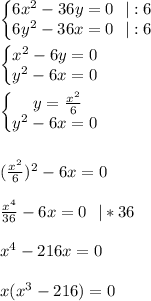
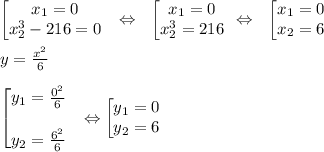
Получаем две ВОЗМОЖНЫЕ (критические или стационарные) точки экстремума: M₁(x₁;y₁) и М₂(х₂;у₂)
в данном случае: M₁(0;0) и M₂(6;6)
1) Проверим точку M₁
для этого находим вторые частные производные функции и подставляем координаты нашей точки:
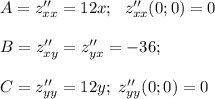
AC-B²=0*0-(-36)²=-36<0 - следовательно экстремума в точке М₁ нет
2) Проверим точку М₂
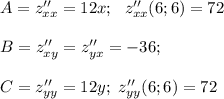
AC-B²=72*72-(-36)²=3888>0 экстремум есть, причем минимум (так как A>0)
Итак, точка минимума М₂(6;6)
Минимум:
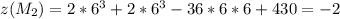
ответ: z=-2 - минимум функции
P.S.
Если AC-B²> 0 и A > 0, то М - точка минимума
Если AC-B²> 0 и A < 0, то М - точка максимума
Если AC-B²< 0, то экстремумов нет
Оценка:
Докажем, что оставшееся на доске число будет нечётным. Посмотрим, как изменяется сумма всех чисел от производимой операции. Пусть сумма чисел до операции равна S, а операция проводится над числами a и b и a ≥ b. Тогда S' = S - a + (a - b) - b = S - 2b. Так как операции нахождения разности проводились над целыми числами, результат будет целым, значит, 2b - чётное число. Изначально сумма всех чисел была равна 2015 * 1007 (нечётное число), значит, после каждой операции она будет оставаться нечётной, откуда последнее оставшееся число будет нечётным. Так как a ≥ b, и a и b - неотрицательные числа, то их разность тоже будет неотрицательна. Значит, число, оставшееся на доске, не будет больше самого большого из изначальных чисел. Тогда наибольшее число, которое могло остаться на доске, равно 2013.
Пример:
Рассмотрим числа k, k+1, k+2, k+3 и k+4. Сперва проведём операцию над числами k+3 и k+4 (получим 1), потом над 1 и k+2 (получим k+1), затем над k+1 и k+1 (получим 0), и, наконец, над k и 0 (получим k). Таким образом мы убираем 4 подряд стоящих числа. Уберём 2012 чисел от 2 до 2013 включительно. Теперь проведём операцию над числами 1 и 2014, получим 2013.
ответ: 2013.
2)30:10=3(год.)-їхав назад
3)3+2=5(год.)
ответ: знадобилось 5 годин