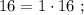
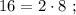
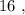т.е.: 
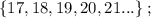
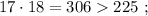
каждое – будет, очевидно, больше чем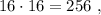 
т.е. больше 
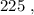а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.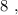
т.е.: 
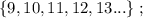
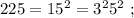
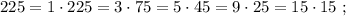
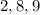и 
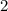и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы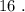 
и никаких натуральных чисел нет. и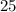 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы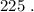 
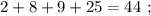
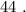
Пошаговое объяснение: Так как уравнение должно иметь ровно 1 корень=> этот корень кратности 3 и значит данный многочлен раскладывается на (bx+-c)^3 и так как корень отрицательный значит берём знак +;
(Bx+C)^3=(Bx)^3+3*(Bx)^2*c+3*bx*c^2+c^3=3x^3-x^2-7x+a-2
Из этого видно, что b= Кубическийкореньиз3=>3x^3-x^2-7x+a-2=3x^3+3*(кубическийкореньиз3)^2*x^2*c+3*кубическийкореньиз3*c^2*x+c^3
-x^2-7x+a-2=3*(кубическийкореньиз3)^2*x^2*c+3*кубическийкореньиз3*c^2*x+c^3 из этого с легкостью можем найти С.
-x^2=3*(кубическийкореньиз3)^2*x^2*c
-1=3*(кубическийкореньиз3)^2*c
С=-1/(3*(кубическийкореньиз3)^2)
=>a-2=(-1/(3*(кубическийкореньиз3)^2))^3
a-2=-1/(27*9)
a-2=-1/243
a=485/243
