a = 9
Пошаговое объяснение:
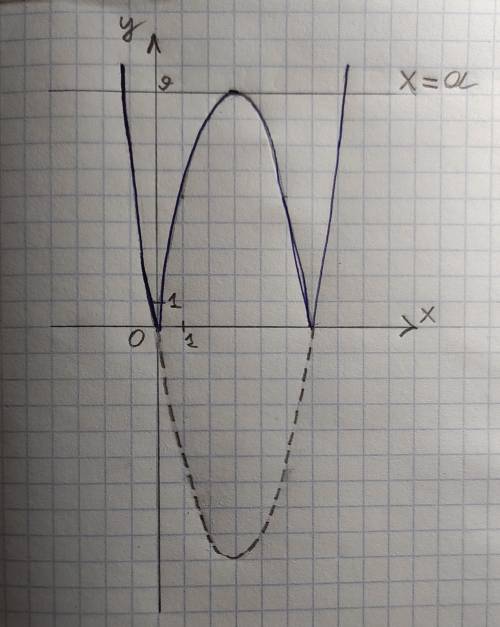
Решим задачу графически. Построим график функции y = |x²-6x|. Для этого сначала построим параболу y = x²-6x, перенеся график y = x² на 3 единицы вправо и на 9 единиц вниз, так как
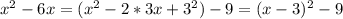
а затем отразим ту его часть, которая расположена ниже оси абсцисс, относительно этой оси. На рисунке во вложении график y = |x²-6x| обведен ручкой.
График функции y = a — прямая, параллельная оси Ox. Абсциссы точек пересечения ее с синей кривой как раз являются корнями заданного уравнения. Видно, что при a = 9 точек пересечения ровно три.
К слову, при значениях a на интервале (0; 9) уравнениe будет иметь целых четыре корня, а если принять, что a>9 или равным нулю, то два. При остальных же значениях a (отрицательных) решений не будет существовать.