Пятьдесят процентов это одна вторая
↓↓↓
Пошаговое объяснение:
1) Количество выпадения четного числа 6
Т.к. на первом кубике 2,4,6 и на втором кубике 2,4,6. ответ С
2) Количество выпадения нечетного числа 6
Т.к. на первом кубике 1,3,5 и на втором кубике1,3,5. ответ С
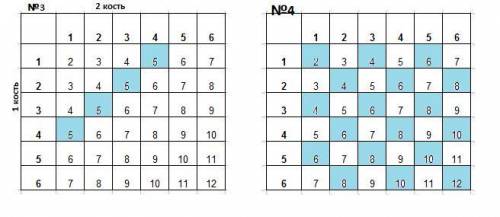
3) Четырьмя может выпасть в сумме число 5
В таблице в каждую ячейку записана сумма числа очков выпавших на первой и второй кости. Нужные ячейки -синие. Их 4.
ответ D
4) Восемнадцатью может выпасть в сумме четное число.
В таблице в каждую ячейку записана сумма числа очков выпавших на первой и второй кости. Нужные ячейки -синие. Их 18.
ответ С
5) Вероятность того, что сумма чисел на двух игральных кубиках будет чётным числом равна 1/2.
Общее число исходов n=36, число благоприятствующих исходов m=18 из п.4. Тогда вероятность события P=m/ n=18 /36=1/2.
ответ A
x ∈ (-∞;-4) ∪ (-1;3)
Пошаговое объяснение:
(x-3)(x+1)(x+4)<0
Это возможно, если нечетное количество множителей отрицательно. Т.е. возможны такие варианты
один множитель отрицательный:
1. x-3>0; x>3; x∈(3;+∞)
x+1>0; x>-1; x∈(-1;+∞)
x+4<0 x<-4; x∈(-∞;-4)
x∈∅
2. x-3<0; x<3; x∈(-∞;3)
x+1>0; x>-1; x∈(-1;+∞)
x+4>0 x>-4; x∈(-4;+∞)
x∈(-1;3);
3. x-3<0; x>3; x∈(3;+∞)
x+1>0; x<-1; x∈(-∞;-1)
x+4>0 x>-4; x∈(-4;+∞)
x∈∅
все три множителя отрицательные:
4. x-3<0; x<3; x∈(-∞;3)
x+1>0; x<-1; x∈(-∞;-1)
x+4>0 x<-4; x∈(-∞;-4)
x∈(-∞;-4);
Окончательно:
x ∈ (-∞;-4) ∪ (-1;3)
1/2часть числа 40 составляет число 20