Пошаговое объяснение:
Обозначаем за х это количество деталей, изготовленных первым рабочим.
Тогда (x + 15) - количество деталей, изготовленных вторым рабочим.
По условию задачи всего было изготовлено 91 деталь.
Составь и реши уравнение (математическую модель данной задачи).
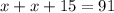
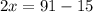
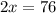
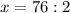
x = 38 деталей - было изготовлено первым рабочим.
Тогда
38 + 15 = 53 деталей - было изготовлено вторым рабочим.
ответ: 53 детали изготовил второй рабочий , а 38 деталей изготовил первый рабочий.
Пошаговое объяснение:
Пусть первая фирма получила х планшетов
Тогда вторая получила (x + 15) планшетов, а третья 2(x + x + 15).
По условию задачи общее число планшетов равно 225.
Решаем полученное уравнение.
x + x + 15 + 2(2x + 15) = 225
2x + 15 + 4x + 30 = 225
6x = 225 - 45
6x = 180
x = 180 : 6
x = 30 планшетов - получила первая фирма
↓
30 + 15 = 45 планшетов - получила вторая фирма
↓
2(30 + 45) = 150 планшетов - получила третья фирма.
ответ: 150 планшетов получила третья фирма.
ответ:-∞ < x < -6, 1 < x < +∞ функция возрастает -6 < x < 1
Пошаговое объясненПроизводная функции у = (х³/3)+(5x²/2)-6x+4 равна:
у = x² + 5x - 6.
Находим критические точки, приравняв производную нулю:
x² + 5x - 6 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=5^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:x₁=(√49-5)/(2*1)=(7-5)/2=2/2=1;x₂=(-√49-5)/(2*1)=(-7-5)/2=-12/2=-6.
Исследуем значение производной вблизи критических точек:
х -6.5 -5.5 0.5 1.5
у 3.75 -3.25 -3.25 3.75.
Если производная меняет знак с + на -, то это максимум функции, если с - на +, то минимум.
На промежутках, где производная положительна, там функция возрастает, а где отрицательна - там функция убывающая