найдём производную функции f(x)=2x³ -3x² -1
f'(x)=6x² - 6x
6x² - 6x= 0
6x(x -1) = 0
1) 6x = 0
x₁ = 0
2) x -1=0
x₂ = 1
график функции f'(x)=6x² - 6x представляет собой квадратную параболу веточками ввех, следовательно,
при х∈(-∞; 0] f'(x)> 0 ⇒ f(x) возрастает
при х∈[0; 1] f'(x)< 0 ⇒ f(x) убывает
при х∈[1; +∞) f'(x)> 0 ⇒ f(x) возрастает
в точке х = 0 локальный максимум y mах = -1
в точке х =1 локальный минимум y min = 2 -3 -1 = -2
Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
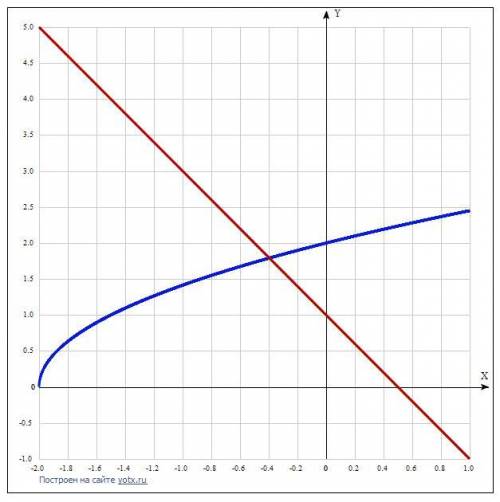
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.