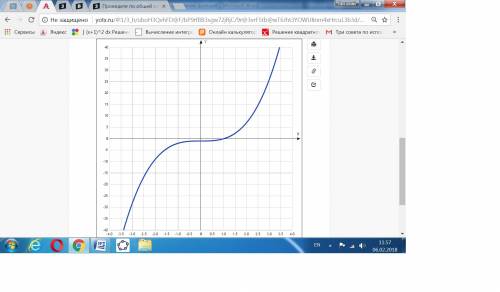
ответ:Дана функция: f(x)=x³−1.
1.Область определения и значений данной функции f: ограничений нет - x ∈ R.
2.Выяснить, обладает ли функция особенностями, облегчающими исследование, т. е. является ли функция f:
а) четной или нечетной: f(-x) = -x³−1 ≠ f(x).
f(-x) = -(x³+1) ≠ -f(x).
Значит, функция не чётная и не нечётная.
б) периодической: функция не периодическая.
3.Вычислить координаты точек пересечения графика с осями координат.
С осью Оу при х =0: у = 0³ - 1 = -1.
С осью Ох при у = 0: 0 = х³ - 1, х³ = 1, х = ∛1 = 1.
4.Найти промежутки знакопостоянства функции f.
Находим производную: y' = 3x².
Так как производная положительна на всей области определения, то функция только возрастающая.
5.Выяснить, на каких промежутках функция f возрастает, а на каких убывает: в соответствии с пунктом 4 функция возрастает от -∞ до +∞.
6.Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точках.
Приравниваем производную нулю; 3х² = 0, х = 0.
Имеем 2 промежутка монотонности функции
На промежутках находят знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Производная y' = 3x² только положительна.
Так как производная не имеет промежутков смены знака, значит, функция не имеет ни минимума, ни максимума.
7.Исследовать поведение функции f в окрестности характерных точек, не входящих в область определения и при больших (по модулю) значениях аргумента: таких точек нет
Пошаговое объяснение:вроде как-то так
вероятность положить 1 белый 5/7*5/12+2/7*7/12, тогда вероятность вытащить белый из 3 урны 7/12*(5/7*5/12+2/7*7/12)(всего 12 из них белых 7)
вероятность положить 2 белых 5/7*7/12=5/12 тогда вероятность вытащить белый из 3 урны 8/12*5/12(всего 12 из них белых 8)
проверка 2/7*5/12+5/7*5/12+2/7*7/12+5/7*7/12 =(2*5+25+14+35)/(7*12)=(10+25+14+35)/84=1)))
складываем вероятности 1/2*2/7*5/12+7/12*5/7*5/12+7/12*2/7*7/12+8/12*5/12=5/84+25/144+14/144+40/144=5/84+79/144
формула бернулли это разложение бинома ньютона
полная формула p^6+6p^5q^1+15p^4q^2+30p^3q^3+15p^2q^4+6pq^5+q^5=1
неудача q это 1-удача (p) q=1-p