Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле:
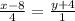
x-8 = 4y+16,
Получаем общее уравнение прямой: х-4у-24 = 0.
2. Написать общее уравнение прямой, если прямая проходит через точку N(-2;6) и имеет угловой коэффициент k=2.
Уравнение с коэффициентом: у = ах+в.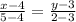
sinx=%2/2
x=45 (град)
2. 3sinx-4sin(в кубе) x+sinx=0
4sinx-4sin (в кубе) x=0
4sinx(1-sin(в квадрате) x)=0
a)sinx=0
b)cos((в квадрате) x=0
cosx=0
3. %3sinx+cosx=0
( (%3sinx+cosx)*2*%3 )/(%3 *2)
sin (120+x) /(%3 *2)=0
sin(120+x)=0
(%3 *2)cosx- (sinx /2)=0
cosx= (sinx /2)/ (%3 *2)
x=arccos90=0
Наверно так)